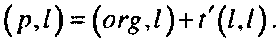
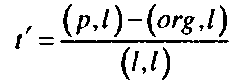
Гпава 3. Простейшие геометрические алгоритмы и структуры
то и любой содержащийся внутри него объект также не пересекает данный объект (или не попадает в область) (рис. 3.3).

Рис. 3.3
В случае, когда описанное тело достаточно простое, осуществление проверки с ним может оказаться гораздо проще (и быстрее), чем с исходным объектом. Это становится особенно выгодным, когда нужно проверить на пересечение два сложных объекта (часто состоящих из множества мелких элементов), - тогда проверка описанных вокруг них тел может дать огромный выигрыш в скорости.
В качестве таких описанных тел (их обычно называют ограничивающими телами) обычно рассматривают простейшие выпуклые тела - сферы или эллипсоиды, прямоугольные параллелепипеды и т. п.
Следует иметь в виду, что если ограничивающие тела для двух объектов пересекаются между собой, то из этого еще не следует факт пересечение исходных объектов (рис. 3.4), поэтому в этом случае может потребоваться проведение дополнительной проверки, более точно учитывающей геометрию исходных тел. Однако это оказывается необходимым только в том случае, когда тест пересечения ограничивающих тел дал положительный результат, что бывает не так часто.
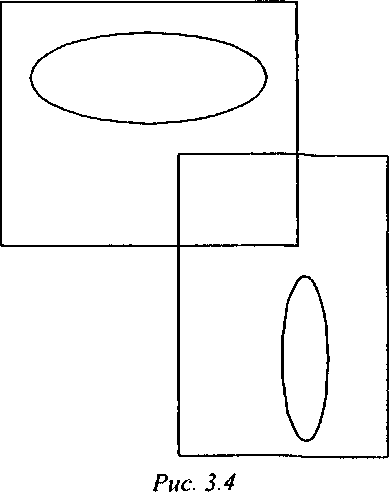
А. В. Боресков. Гоафит трехмерной компьютерной игры
Самым простым ограничивающим телом является сфера, описанная вокруг заданного объекта (или набора его вершин) (рис. 3.5).
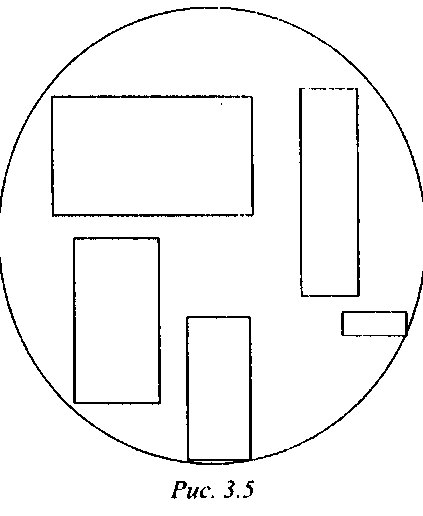
Простейшим способом построения такой сферы является нахождение средней точки заданного набора вершин и вычисление максимального расстояния от него до всех точек набора.
Пусть задан набор точек у0, v,,…,уп_, . Тогда в качестве центра сферы можно взять точку
а в качестве ее радиуса Проверка на попадание точки р внутрь ограничивающей сферы крайне проста"images/tmpFE1D-80.png">
(3.2)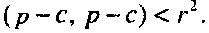
(3.3)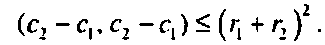
(3.4)