float vNew = (float) fabs ( operator [] ( i ) );
if ( vNew > val ) {
val = vNew; axis = i;
}
}
return axis;
}Особенно эффективно применение данного подхода, когда нужно быстро оценить расстояние до группы объектов вдоль одного и того же вектора, - тогда по этому вектору один раз вычисляется главная ось и расстояние определяется вдоль нее.
Нахождение расстояния от точки до прямой Пусть заданы точка р(х, у, z) и прямая org + t-l и требуется найти расстояние от данной точки до этой прямой. Решение этой задачи в двухмерном случае приводится в [1]. Ниже приводится общее решение, пригодное для трехмерного пространства.
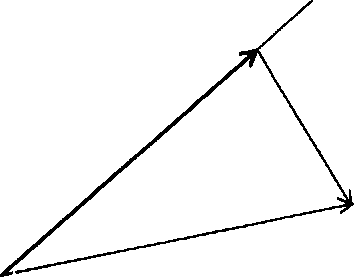
Для начала спроектируем точку р на прямую, представив ее как сумму вектора вдоль прямой и вектора, ортогонального направляющему вектору прямой:
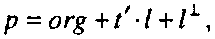
где вектор Iі перпендикулярен вектору / (рис. 3.2).
Рис. 3.2
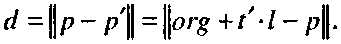
Для определения параметра Ґ умножим скалярно это уравнение на вектор /. Тогда мы получим Отсюда легко определяется параметр г' проекции точки р на прямую: Тогда искомым расстоянием будет расстояние между точками р и р'.
Ограничивающие тела Одной из наиболее частых операций, которые будут встречаться в графической (да и не только в ней) части игры, является проверка объектов на пересечение между собой, попадание в заданную область или выполнение каких-либо других условий, связанных в положением объектов.
Поскольку эта задача встречается очень часто, то ее правильная реализация может заметно повысить быстродействие всей системы в целом. В этой главе мы рассмотрим основные алгоритмы и структуры данных для эффективного осуществления таких проверок, а также примеры их реализации.
Одной из самых простых, но очень часто встречающихся структур, являются ограничивающие тела (bounding volumes). Их использование основывается на следующем крайне простом наблюдении: если вокруг сложного объекта описать некоторое тело, полностью содержащее его в себе, то если это тело не пересекает другой объект (или не попадает в заданную область),
