Еще одной часто встречающейся операцией над ограничивающим телом является добавление новой точки (или ограничивающего тела) к заданному гелу.
При добавлении точки р к заданной ограничивающей сфере (с, г) центр сферы обычно не изменяется, а в качестве нового радиуса берется шах (г, \\с-р\\).
При объединении двух ограничивающих сфер (с,, /\) и (с2, г2) параметры (с, г) для новой сферы, содержащей их обе внутри себя, задаются следующими формулами (рис. 3.6):
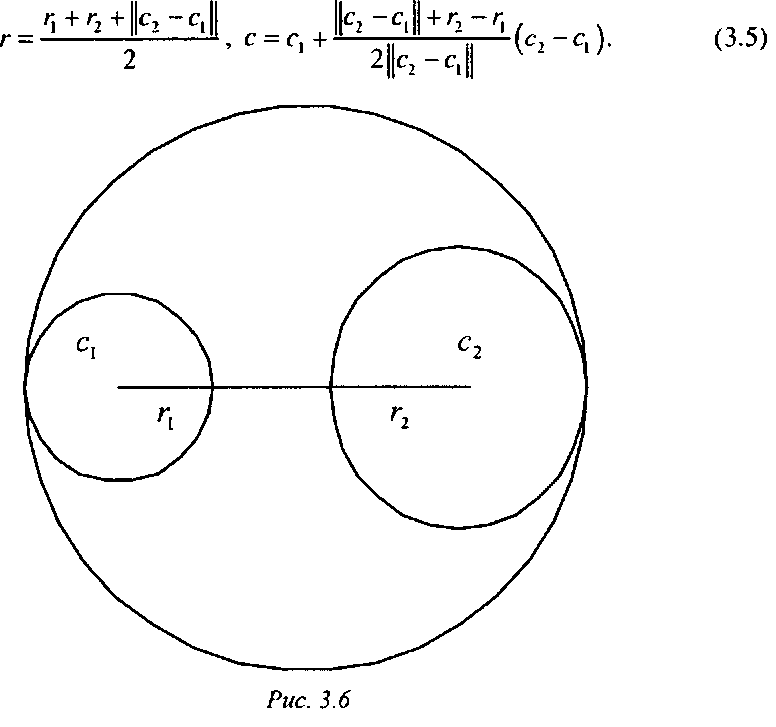
Также часто встречается необходимость проверить на попадание ограничивающей сферы в заданное полупространство (или пересечение полупространств). Пусть полупространство задается неравенством (їх, р) + сі>0, а сфера - набором (с, г).
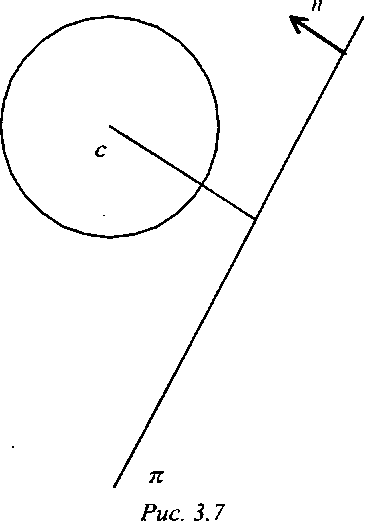
Тогда, если расстояние от центра сферы до плоскости я: (и, р) + а'=0
больше радиуса сферы, то она целиком лежит в том полупространстве, в котором лежит и ее центр (рис. 3.7). В противном случае сфера лежит сразу в обоих полупространствах.
Расстояние от центра сферы с до плоскости я:(и, р) + а"=0 может быть
найдено по следующей формуле (при условии, что вектор нормали п является единичным):
<й#(с, я) = (с, п) + с1. (3.6)
Описанные методы можно собрать вместе и реализовать в виде следующего класса:
class BoundingSphere {
private:
Vector3D center;
float radius;
float radiusSq; public:
BoundingSphere ( const Vector3D& c, float r ) : center ( c ), radius ( r )
{
radiusSq = r * r;
}
BoundingSphere ( const Vector3D * v, int n ) ;
const Vector3D& getCenter () const {
return center;
}
float getRadius () const {
return radius;
}Простейшие геометрические алгоритмы и структуры
void addPoint ( const Vector3D& p ) {
float rSq = (p-center).lengthSq ();
if ( rSq > radiusSq ) {
radiusSq = rSq;
radius = (float) sqrt ( radiusSq ) ;
}
}
void merge ( const BoundingSphere& s );
bool contains ( const Vector3D& p ) const {
return (p-center).lengthSq () <= radiusSq;
}
bool contains ( const BoundingSpherefc s ) const {