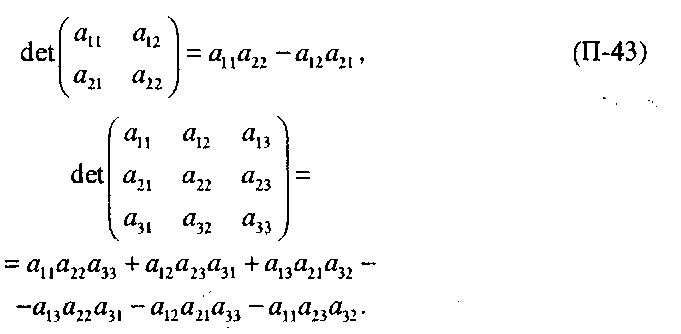
Для определителей справедливо следующее соотношение: с1е1(АВ) = с!е1Ас1е1б. (П-44) Матрица называется вырожденной, если ее определитель равен нулю.
Для невырожденной квадратной матрицы А можно построить квадратную матрицу А'1 такого же размера, называемую обратной матрицей к П-Для обратной матрицы справедливо следующее соотношение: АА1=А'1А = 1. (П-45)
Соотношение Ах = Ь. (П-46)
называется системой линейных алгебраических уравнений порядка и . Необходимым и достаточным условием ее однозначной разрешимости для любой правой части Ь является отличие от нуля определителя матрицы этой системы (ае1 А Ф 0). В этом случае ее решение может быть записано в виде х = А'1Ь. (П-47)
Необходимым и достаточным условием существования нетривиальных (т. е. отличных от нулевого вектора) решений у однородной системы Ах - 0 является как раз равенство нулю ее определителя ае1 А = 0 (в противном случае нулевое решение является единственным).
Определение. Если для ненулевого вектора х и числа X (вещественного или комплексного) выполнено следующее свойство: Ах=Хх, (П-48)
то X называется собственным числом матрицы А, соответствующим собственному вектору X.
Обратите внимание, что если х - собственный вектор матрицы А, то для любого вещественного а вектор ах также является собственным вектором для данной матрицы, причем он соответствует тому же самому собственному числу X.
Соотношение (П-48) можно переписать в виде
(А-Х1)х = 0. (П-49)
Это соотношение является однородной системой линейных алгебраических уравнений, и для существования у нее нетривиальных решений необходимо и достаточно обращения в нуль ее определителя с1е1 (Л - Л/) = 0. Данный определитель является многочленом степени п относительно исПриложение. Векторная и матричная алгебра комого собственного числа X и называется характеристическим многочленом матрицы Л: рЛ(Х) = йе1(А-Х1). (П-50)
Согласно основной теореме алгебры данное уравнение имеет ровно п корней с учетом кратности, но эти корни могут быть комплексными.
