где скобки обозначают, что речь идет о всей совокупности элементов, а не об одном конкретном элементе.
Если все элементы матрицы равны нулю, то такая матрица называется нулевой и обозначается как О .
Матрица, для которой т = п , называется квадратной.
Квадратная матрица, где все элементы, не лежащие на главной диагонали, равны нулю, а на главной диагонали лежат единицы, называется единичной и обозначается как / (или Е).
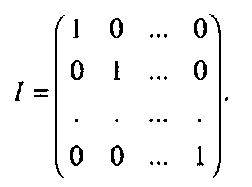
(П-32)
Для двух матриц А и В одинакового размера тхп можно ввести операцию сложения, определив сумму двух матриц как матрицу, состоящую из сумм соответствующих элементов обеих матриц.
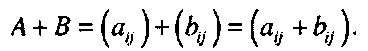
(П-33)
Легко, как и в случае векторов, убедиться в выполнении коммутативности и ассоциативности, а также в том, что добавление нулевой матрицы О не изменяет исходную матрицу.
Также можно ввести операцию умножения матрицы на вещественное число, определив ее поэлементно.
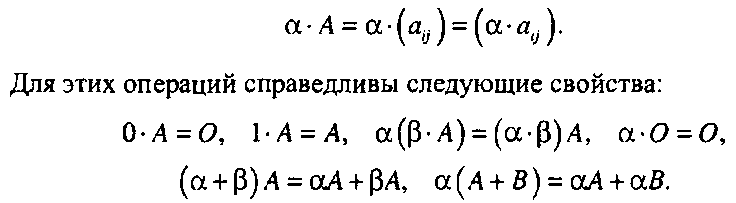
(П-34)
(П-35)
Кроме вышеприведенных операций можно ввести операцию транспонирования, где матрице А размера тхп становится в соответствие матрица А7 размера пхт, полученная путем "переворачивания" матрицы вдоль ее главной диагонали: Также для квадратной матрицы можно определить след матрицы, определив его как сумму диагональных элементов.
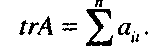
(П-37)

Приложение. Векторная и матричная алгебра Если имеются две матрицы А и В, размера тхп и «х/ соответственно, то можно определить матрицу С размера тх1, являющуюся произведением этих матриц. Элементы этой матрицы определяются при помощи следующей формулы:
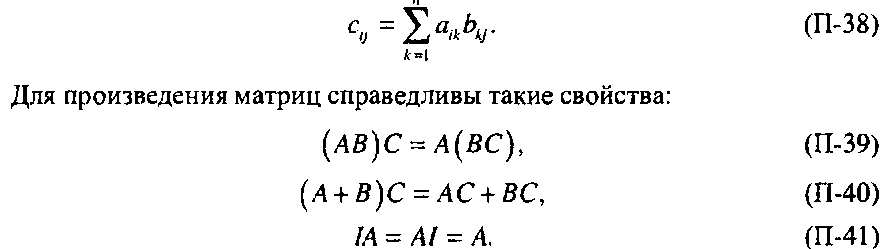
В общем случае АВ ФВА , даже если размеры матриц позволяют произвести оба умножения.
Вектор можно рассматривать как матрицу из одного столбца, т. е. матрицу размера шх 1; таким образом, можно умножить матрицу пхт на вектор размера т х 1.
Для скалярного произведения выполняется следующее свойство:
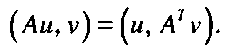
(П-42)
Для квадратной матрицы А можно ввести числовую характеристику, называемую определителем и обозначаемую как |а| или del А. Ниже приводятся формулы для вычисления определителей матриц 2x2 и 3x3.
