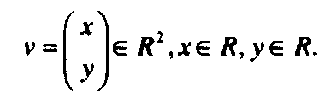
(П-1)
Такой столбец мы будем называть двухмерным вектором. Для двухмерных векторов можно естественным образом ввести операцию сложения, определив ее покомпонеитио.
(П-2)
Также можно ввести операцию умножения вектора на произвольное вещественное число:
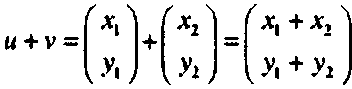
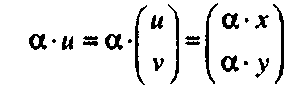
(П-3)
По аналогии с пространством двухмерных векторов Я2 можно ввести пространство «-мерных векторов Я", состоящее из упорядоченных наборов из л вещественных чисел.
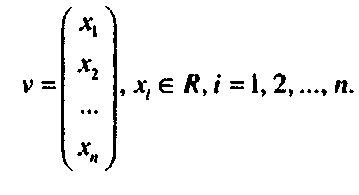
(П-4)
Приложение. Векторная и матричная алгебра Для векторов из Я" также можно ввести операции сложения и умножения на число аналогично соответствующим операциям для двухмерных векторов.
Несложно убедиться в выполнении следующих простых свойств этих операций:
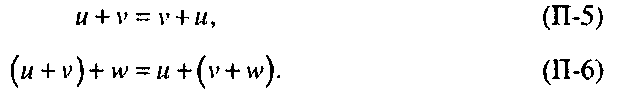
Свойство (П-5), справедливое для двух любых векторов из Я", называется коммутативностью, а свойство (П-6) называется ассоциативностью. Эти свойства непосредственно следуют из аналогичных свойств для вещественных чисел и определения операции сложения векторов в й".
Также легко заметить, что существует вектор 0 (и притом единственный), такой,что и этот вектор состоит из одних нулей.
Для любого вектора и можно определить вектор -и, такой, что
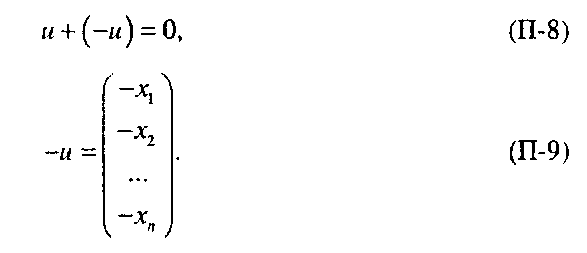
Умножение векторов на вещественные числа также обладает рядом свойств.

Также можно определить скалярное произведение (dot product) для произвольных двух векторов и и v. Оно обычно обозначается как и v или (и, v) и определяется следующей формулой:

Приложение. Векторная и матричная алгебра В случае трехмерного пространства r? можно также ввести понятие векторного произведения (cross product) двух векторов и и v, определив его следующим образом:
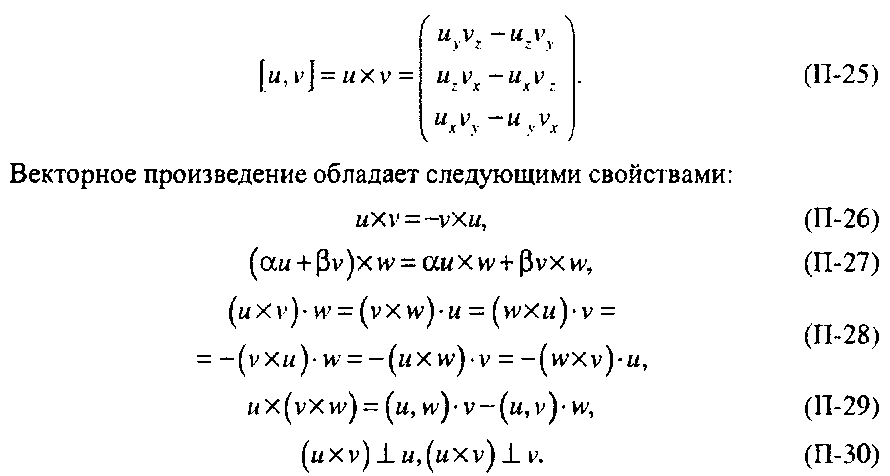
Обратите внимание, что длина векторного произведения векторов равна удвоенной площади треугольника, построенного по этим векторам
(По аналогии с вектором, представляющим собой столбец вещественных чисел, можно ввести понятие матрицы как прямоугольной таблицы вещественных чисел:
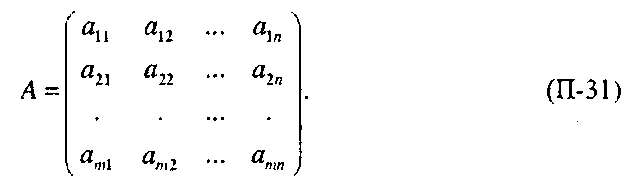
Числа т и п называются размером матрицы, множество всех матриц
размера тхп обозначается Л"'". Иногда матрицу А обозначают как («у),
