Второй пример векторного пространства- это пространство алгебраических векторов, т.е. совокупностей п скаляров. Как правило, скалярами являются действительные или комплексные числа. В таком пространстве вектор определятся как
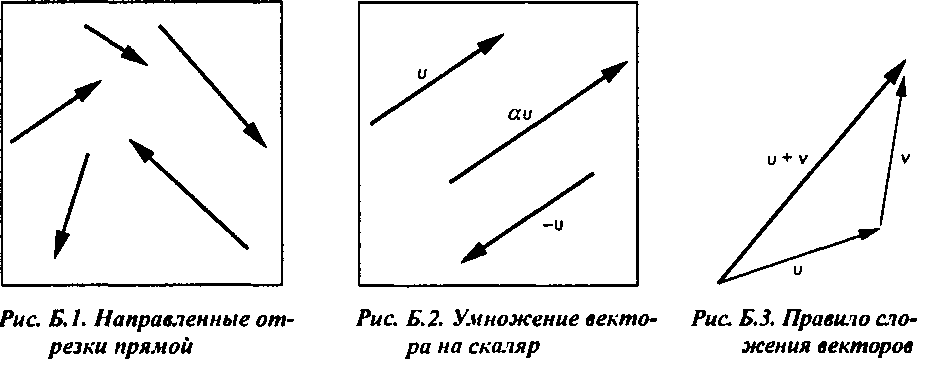
*' = (vv:.....»'„)Операции умножения вектора на скаляр и сложения векторов определяются соотношениями
m + \' = (u1,m,,…,/<„) + (i,i,v,.....v„) = (і/, + v,, и2 + \>2, m„+v(|),
ocv = (ocv,,ocv,.....oc\>„).Такое векторное поостранство принято обозначать R", и для манипуляций с векторами в нем используется математический аппарат матричной алгебры, который будет кратко описан в приложении В.
Базовой концепцией векторного пространства является линейная независимость векторов. Линейной комбинацией п векторов и\, и,и„ называется вектор вида и - ос,//, + ос,м, + … + ос„н„. Если соотношение ОС,//, + ОС,//, +… + ОС,,//,, = О
удовлетворяется только единственным множеством скаляров а, =а, = …ос„ =0.
то векторы щ, и,и„ являются линейно-независимыми. Наибольшее количество линейно-независимых векторов, которое может быть найдено в данном векторном пространстве, определяет размерность этого пространства. В «-мерном векторном пространстве любое мно-
Б.2. Векторное пространство жество п линейно-независимых векторов образует базис этого пространства. Если г,. г„ есть базис пространства У, то произвольный вектор V можно единственным способом представить в виде линейной комбинации векторов базиса: Множество скаляров {(3,} называется разложением вектора г по базису гь т;, г„ (часто также используется термин представление вектора г в базисе гь г2, г„). Если множество і'і, г':, г'„ представляет собой другой базис в этом же пространстве (количество векторов в базисе для данного пространства фиксировано), то существует разложение вектора г по этому базису: у = $У]+&У2 + … + Р',\','.
Разложения вектора по разным базисам «-мерного векторного пространства связаны матрицей М размера п х п, такой, что
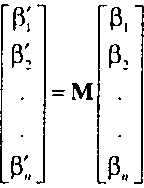
Свойства матриц М мы рассмотрим в приложении В. Такая матрица позволяет изменять представление вектора с помощью линейного преобразования, которое реализуется с помощью только вычислительных операций над скалярами в процессе умножения матриц. Обобщая, можно утверждать, что если известен базис (или базисы) векторного пространства, то далее все манипуляции происходят только с разложениями векторов по базису (или по базисам) этого пространства. Если скаляры в данном пространстве являются вещественными числами, то все операции над /7-мерными векторами (наборами п чисел) можно свести к операциям матричной алгебры.
