Б.З. Аффинное пространство Строго говоря, в векторном пространстве отсутствуют такие понятия, как положение и расстояние. Если в качестве векторного пространства для решения геометрических задач использовать пространство отрезков прямых, то мы встретимся со множеством сложностей, поскольку векторы в нем являются свободными, т.е. как и физические векторные величины, имеют модуль (длину) и направление, но не имеют точки приложения. Векторы, показанные на рис. Б.4, являются в векторном пространстве идентичными объектами.
Система базисных векторов, которая позволяет представить любой вектор в данном пространстве в виде набора коэффициентов разложения по этому базису, образует систему координат пространства. На рис. Б.5,а показаны три базисных вектора, исходящие из определенной точки пространства, называемой началом этой системы координат. Те векторы, которые показаны на рис. Б.5,6, идентичны базисным векторам, поскольку в векторном пространстве все векторы являются свободными. В результате в векторном пространстве отсутствует возможность определить эту особую точку, к которой должны быть "привязаны" базисные векторы.
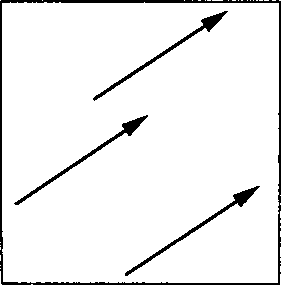
Рис. Б.4. Идентичные свободные векторы
Приложение Б. Абстрактные пространства в компьютерной графике
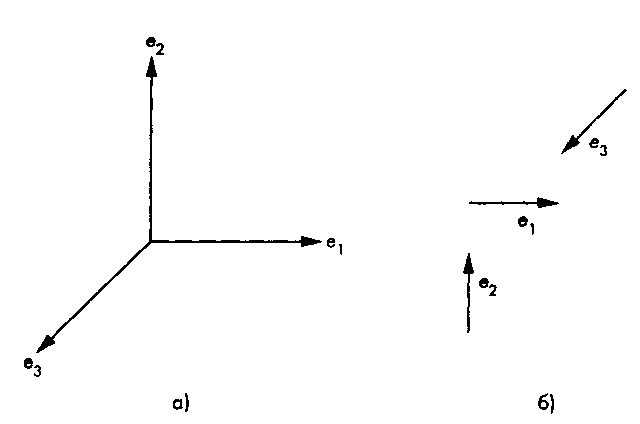
Рис. Б. 5. Система координат: а - базисные векторы, "привязанные" к точке начала координат; б - свободные базисные векторы
Эта проблема разрешается вводом в векторное пространство еще одного типа объектов - точки. Такое "дополненное" векторное пространство получило название аффинного. В аффинном пространстве определено множество точек (Р, (), Я,…), и единственная операция над ними- вычитание точек, результатом которой является вектор. Если Р и ()- две произвольные точки, то результат операции вычитания
\> = Р-()
есть вектор в пространстве V. Следовательно, для любого вектора г и любой точки Р можно отыскать такую точку <2 , для которой будет справедливо приведенное выше соотношение. Эта операция, производная от базовой операции вычитания точек, называется операцией сложения вектора и точки
