Вычислив координаты точки (точек) пересечения проецирующего луча с поверхностью, мы можем применить к этой поверхности одну из моделей закрашивания. Нужные для этого компоненты вектора нормали можно найти с помощью частных производных функции g в точке пеоесечения:
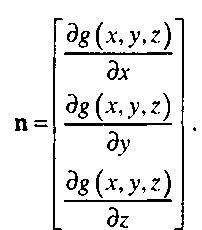
Обычно при отображении таких поверхностей нас не очень заботит проблема глобального освещения. Следовательно, нет необходимости вычислять параметры теней, т.е. опреде лять, освещается ли данная точка поверхности от определенного источника, или параметры отраженных лучей. Для сцен, состоящих из простых квадратичных поверхностей, приведение лучей является не только способом отображения, но и позволяет проанализировать видимость поверхности и часто используется в сочетании с моделями, созданными в рамках конструктивной геометрии тел. Но для функций, более сложных, чем квадратичные, объем вычислений, требуемых для определения точки пересечения проецирующего луча с поверхностью, становится основным лимитирующим фактором, и приходится искать альтернативные методы отображения.
Сформулируем более общую постановку задачи - отображать не поверхности, а объемы, т.е. рассматривать не поверхность, описываемую уравнением g(x, у, г) = 0, а скалярное поле т\х, у, г), определенное в каждой точке пространства. Если нас интересует только определенное значение функции /, скажем значение с, то в этом случае мы имеем дело с задачей отображения изоповерхности скалярного поля: У, =) =А*, у,:)-с = 0.
Иногда вполне достаточно сформировать изображение одной изоповерхности. В частности, это относится к приложениям компьютерной томографии, где пользователя интересуют области с определенным уровнем поглощения тканями рентгеновских лучей. Но существуют и приложения, в которых необходимо выводить на экран изображения нескольких изоповерхностей.
Ниже мы рассмотрим метод построения изоповерхности скалярного поля, заданного объемным множеством данных - выборок, измеренных на равномерной сетке. Этот метод получил название метода маркированных кубиков и является расширением метода маркированного квадрата на трехмерное пространство независимых переменных.
