g(x,y,=) = 0,где функция g представляет собой некоторое аналитическое выражение. Множество точек, удовлетворяющих этому уравнению, образуют одну или несколько трехмерных поверхностей. Общеизвестными примерами являются сфера, плоскость, квадратичные поверхности, тор радиуса г, имеющий радиус поперечного сечения а:
0.(х- + у + Z' - Г - а)' - 4а (Г - z~)
Хотя функция g и позволяет выяснить, принадлежит ли точка (х, у, z) заданной поверхности, при построении поверхности она может играть только вспомогательную роль. Нам придется самостоятельно изобрести метод построения поверхности.
Один из способов основывается на упрощенной форме трассировки лучей, который получил название приведения луча (ray casting). На рис. 12.17 показаны наблюдатель, поверхность, соответствующая функции, и картинная плоскость. Любой проецирующий луч можно описать параметрическим уравнением р(0 = ро + td.
Визуализация данных научных исследований
Перепишем это уравнение в виде системы уравнений для компонентов: х(1) =х0 + 1с1х,
2(/) = Г0 + td:.
Подставив их в неявное уравнение поверхности, получим скалярное уравнение относительно неизвестной /: ф0 + у0 + tdy, 10 + td:) = = 0.
Решением уравнения является точка пересечения проецирующего луча с поверхностью, причем решение может быть не единственным. Последнее означает, что луч пересекает поверхность многократно. Если g- простая функция, например уравнение квадратичной поверхности или тора, то уравнение м(0 можно решить аналитически. Если g представляет квадратичную поверхность, то и является квадратным уравнением относительно неизвестной / и имеет не больше двух действительных корней, которые находятся по известному алгебраическому выражению, знакомому всем со школьной парты. Если же функция g имеет более сложный вид, например полинома более высокой степени, или включает тригонометрические или экспоненциальные функции, то решать уравнение придется численными методами.
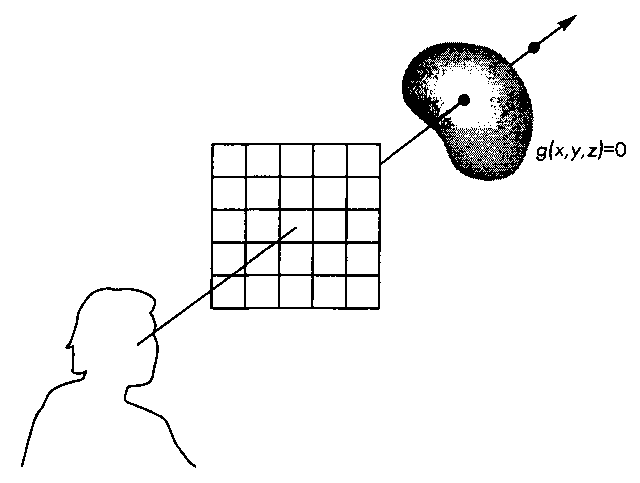
Рис. 12.17. Приведение луча при отображении поверхности, заданной функцией в неявном виде
