12.4. Изоповерхности и метод маркированных кубиков Пусть имеется массив выборок {/11к} скалярного поля Лх, у, г)- множество вокселей. Требуется по этим выборкам построить изоповерхность в форме полигональной сети. Для заданного значения с может существовать единственная изоповерхность, ни одной изоповерхности или несколько. Учитывая, что графическая система лучше всего справляется с задачей отображения трехмерных треугольников, разработаем метод, который позволит отыскать вершины изоповерхности и аппроксимировать ее множеством треугольников. Этот метод получил наименование метода маркированных кубиков.
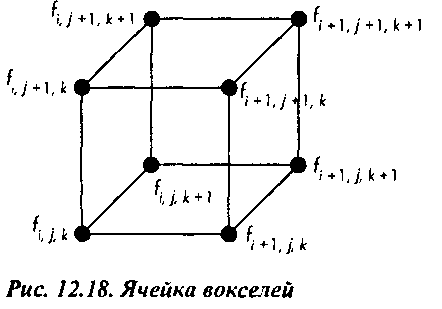
Будем считать, что выборки сняты на равномерной сетке, узлы которой совпадают с центрами вокселей. Если это не так, то всегда можно использовать ту или иную процедуру интерполяции и получить из исходного массива неструктурированных данных множество вокселей (см. упр. 12.7). Восемь соседних узлов пространственной сетки образуют одну ячейку в форме кубика (рис. 12.18). Воксель (/',_/, к) в углу этой ячейки имеет значение /ик. Теперь на основе имеющихся значений вокселей следует проанализировать, проходит ли изоповерхность через данную ячейку, и если проходит, то отыскать координаты вершин соответствующего участка.
Для данного значения уровня изоповерхности с можно промаркировать черным и белым цветом вершины ячейки, в зависимости от того, превышает значение соответствующего вокселя с или нет. Существует 28=256 возможных вариантов маркировки отдельной ячейки. Но приняв во внимание имеющуюся симметрию отдельных вариантов, все разнообразие сводится к
Визуализация данных научных исследований
14 уникальным случаям (рис. 12.19) . Точки пересечения поверхности с ребрами ячейки можно вычислить, используя тот же метод интерполяции, который применялся при обработке квадратных ячеек в методе маркированных квадратов (см. раздел 12.2). После определения координат точек пересечения формируется участок изоповерхности в виде одного или нескольких треугольников (рис. 12.20).
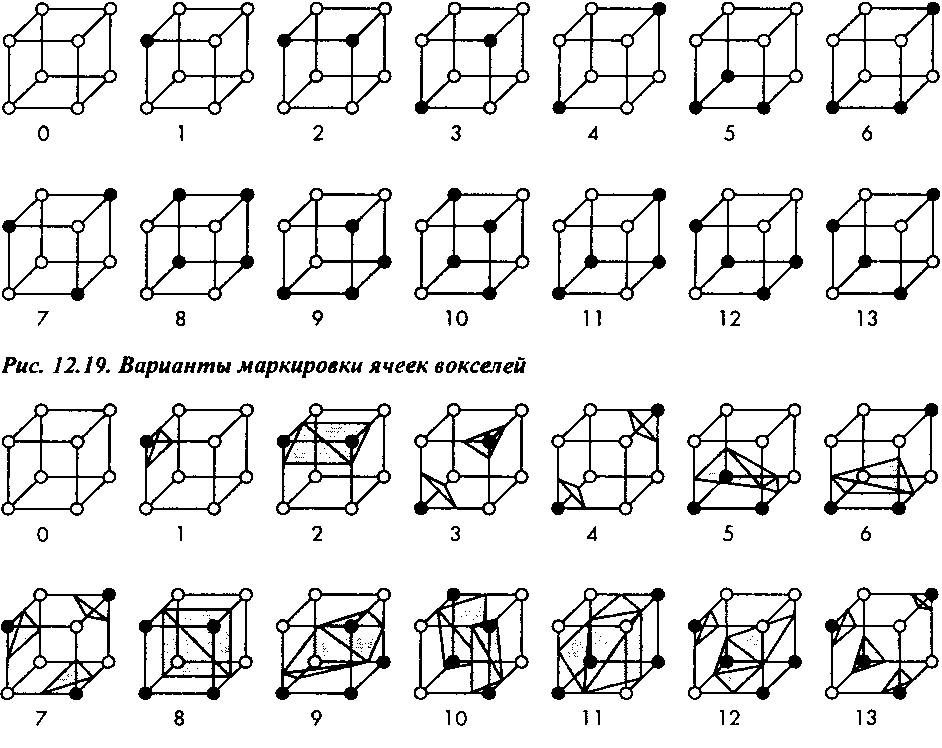
Рис. 12.20. Элементарные участки изоповерхности в ячейках вокселей
