11.7.2. Размерность фрактала Рассмотрим линейный сегмент единичной длины, единичный квадрат и единичный куб (рис. 11.19). При любой приемлемой формулировке понятия размерность линейный сегмент, квадрат и куб должны оставаться одно-, двух- и трехмерными объектами соответственно. Предположим, в нашем распоряжении есть измеритель с разрешением И, где И=\1п- наименьшая единица длины, воспринимаемая прибором. Положим, что п - целое число. Разделим объекты на подобные в терминах значения И, как показано на рис. 11.20.

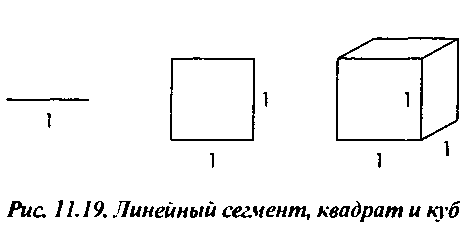
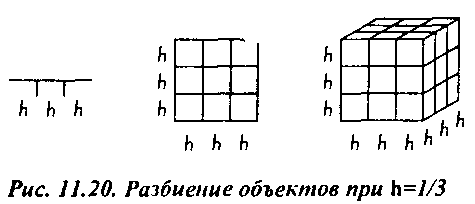
Линейный сегмент разобьем на к=п идентичных сегментов, квадрат - на к=п более мелких квадратов, а куб - на к=п более мелких кубиков. В любом случае можно утверждать, что новый объект сформирован в результате сжатия исходного с коэффициентом И и подстановкой на место исходного к раз. Пусть d - размерность любого из этих объектов. В процессе разбиения сохраняется сумма всех компонентов, и математически для любого объекта это выражается равенством Л = */Г'=1.

Процедурные методы

Решая это уравнение относительно d, получим выражение для размерности фрактала {fractal dimension):

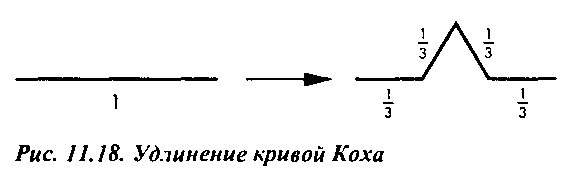
d = - In /I

Другими словами, размерность фрактала некоторого объекта есть мера оценки количества подобных объектов, формируемых в одном цикле разбиения. Рассмотрим теперь кривую Коха. При ее разбиении создается четыре подобных объекта, каждый из которых втрое короче. Соответствующее уравнение для размерности фрактала имеет вид

In 4

d= - = 1.26186. 1пЗ

Повторим аналогичные рассуждения в отношении узора Серпинского. Один цикл разбиения представлен графически на рис. 11.21. В каждом цикле стороны треугольника делятся пополам и формируется объект, в который включаются три из четырех образовавшихся треугольников. Следовательно, получим

d= - = 1.58496. In 2

В обоих случаях видно, что в результате разбиения формируется объект, который занимает больше пространства, чем кривая, но меньше, чем площадь области, ограниченной исходным объектом. Можно сформировать и трехмерный аналог узора Серпинского. Исходным объектом в этом случае будет тетраэдр. В процессе разбиения его грани делятся как объекты двухмерного узора (рис. 11.22). В сформированном объекте остаются четыре малых тетраэдра, а область в середине исходного тетраэдра удаляется. В результате получим значение размерности фрактала трехмерного узора Серпинского:

⇐ Предыдущая| |Следующая ⇒