При заданных внешних силах g и состоянии системы частиц и в момент времени / можно вычислить
ёг=[ м3 м4 м5 ~кЛ% -Ы> -Ы. и9 и10 ии Ых Ы. ^.
Здесь к - постоянная упругости пружины, а а"х, с!х., а1. - компоненты нормированного вектора между а и Ь. Следовательно, сначала необходимо вычислить
Программа решения обычных дифференциальных уравнений требует, чтобы мы вычисляли функцию g для экстраполяции состояния и на будущее. Можно разработать набор таких программ, основываясь на теореме Тейлора. Простейший метод этой группы известен как метод Эйлера. Предположим, что интегрируется выражение на коротком промежутке времени И:
|('+''ш/т = и(/ + п) - и(/) = |'+'^(и,т)^т.
Если И мало, можно заменить значение g на интервале [/, значением g в момент /; следовательно, и(1+И)« и(0+^(и(/), 0.
Из этого выражения следует, что для приближенного вычисления значения и{(+Н) используется значение производной в момент времени / (рис. 11.5).
Это выражение учитывает два первых члена разложения функции в ряд Тейлора; мы можем записать его в виде и(1 + п) = и(1) + пй(!) + 0(п2) = и(() + п£(и({),г) + 0(п2).
Из этого выражения видно, что ошибка аппроксимации пропорциональна квадрату шага интегрирования.
Реализовать этот метод не представляет особого труда. Нужно вычислить значения сил (как внешних, так и сил взаимного влияния частиц системы друг на друга) в момент времени /, вычислить массив обобщенных сил g, умножить его на И и добавить к массиву теку-
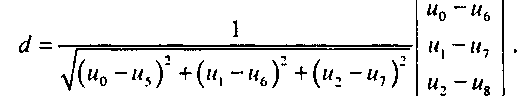
11.4. Решение системы уравнений щего состояния. По этому методу в итерационном цикле вычисляются состояния системы и в последующие моменты времени 1+2И, 1+З/1,… . Основные вычисления - определение массива обобщенных сил в каждый момент времени.
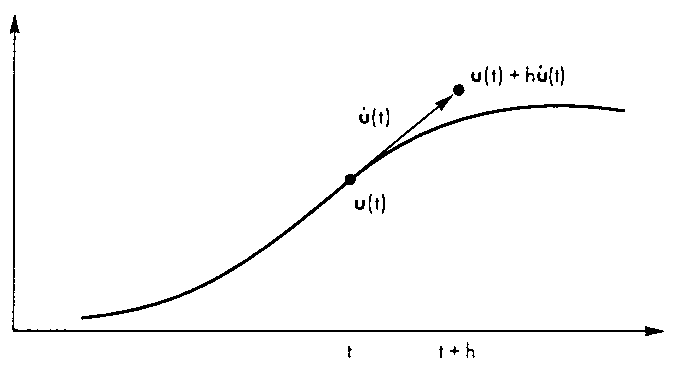
Рис. 11.5. Приближенное решение дифференциального уравнения по методу Эйлера Применение метода Эйлера требует тщательного выбора шага интегрирования, поскольку от него зависит точность результата и устойчивость итерационной вычислительной процедуры. Точность вычисления пропорциональна квадрату шага интегрирования. Следовательно, для повышения точности нужно уменьшать шаг, что увеличивает количество циклов итерации и соответственно время решения. Но еще более серьезные опасения вызывает проблема устойчивости вычислительной процедуры. При переходе к очередному циклу у нас появляются ошибки, источниками которых являются, во-первых, использование для приближения только первых членов разложения в ряд Тейлора, а во-вторых, ограниченная разрядность компьютера. Эти ошибки могут либо компенсировать друг друга, либо, наоборот, суммироваться и, следовательно, накапливаться. Такое поведение вычислительного алгоритма принято называть вычислительной неустойчивостью. К счастью, в большинстве задач, связанных с анализом состояния системы материальных точек, используются достаточно простые модели сил, а потому при правильном выборе шага интегрирования неустойчивость не отмечается. Потенциально наиболее подверженной вычислительной нестабильности оказывается модель, в которой учитываются силы упругого взаимодействия. Дело в том, что при определенных значениях коэффициентов жесткости, входящих в уравнения Гука, даже точное решение имеет колебательный характер, а потому наложение на него ошибок численного интегрирования делает вычислительный алгоритм склонным к "самовозбуждению".
