Существуют два подхода к решению проблемы вычислительной неустойчивости. Один состоит в том, чтобы отказаться от использования метода Эйлера. Анализ таких методов выходит за рамки нашего курса, и мы отсылаем читателей к специальной литературе по численным методам. Другой подход состоит в том, чтобы сохранить в общих чертах метод Эйлера, но внести в него некоторые изменения, уменьшающие накопление ошибок при переходе к очередному циклу. Мы кратко остановимся на одном из методов такой модификации, который даст читателем общее представление о целом семействе подобных методов.
Предположим, что, как и раньше, мы начинаем с интегрирования дифференциальных уравнений на коротком интервале, чтобы получить
Но на этот раз будем использовать при интегрировании усредненное значение на интервале [/, г+И]:
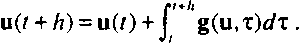
Процедурные методы
f'*" g(u, x)dx «| (g (u (/), /) + g (u (/ + Л), / + A))
Теперь появляется другая проблема - в нашем распоряжении нет значения g(u(M-A), t+h), мы располагаем только значением g(u(/), /). Для приближенного вычисления g(u(t+h), t+h) воспользуемся все тем же методом Эйлера:
g(u(/+A), t+h) = g(u(/)+Ag(u(0, /), t+h).Этот метод известен под названием усовершенствованного метода Эйлера (improved Eider method) или метода Рунге-Кутта второго порядка (Runge-Kulta method of order 2). Обратите внимание на то, что в одном и том же цикле (при переходе от t к t+h) значение g нужно вычислять дважды. Однако, если проанализировать ошибку согласно теореме Тейлора, то окажется, что она имеет порядок 0(h3). Следовательно, хотя на каждом шаге приходится делать больше вычислений, размер шага можно увеличить (а количество циклов соответственно уменьшить) и в итоге даже добиться более высокой производительности. Можно и далее повышать порядок формул Рунге-Кутта, увеличивая тем самым точность вычислений на каждом шаге. Наиболее распространенным в настоящее время для решения обычных дифференциальных уравнений является метод Рунге-Кутта четвертого порядка, который предполагает четырехкратное уточнение значения g в течение одного шага интегрирования, но обеспечивает при этом точность порядка 0(h4). В последнее время разработаны методы этой же группы, которые автоматически подстраивают интервал интегрирования в процессе решения таким образом, чтобы обеспечивалась устойчивость итерационного процесса.
