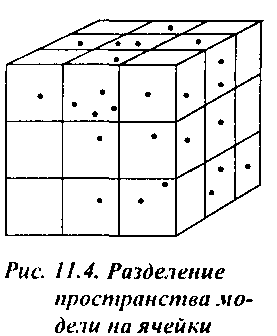
Размеры ячеек выбираются с учетом характера взаимодействия - обратной пропорциональности между величиной силы и квадратом расстояния. При оптимально выбранных размерах ячеек для вычисления сил притяжения и отталкивания, которые действуют на частицу, находящуюся в некоторой ячейке, достаточно анализировать только частицы, находящиеся в этой же ячейке и в соседних с ней. Если такая кластеризация пространства модели допустима, оценка сложности вычислений будет иметь вид 0{п), а не 0(п2). Но, естественно, кластеризация требует накладных расходов. Частицы могут переходить из одной ячейки в другую, а потому время от времени необходимо выполнять их сортировку. Сложность состоит в том, что приходится изобретать подходящую структуру данных для описания ячеек и хранения информации о частицах.
Другой подход состоит в том, что взаимодействие частиц друг с другом заменяется учетом взаимодействия частица и силового поля. Например, если необходимо определить силу гравитации, действующую на частицу, находящуюся на поверхности Земли, используется значение гравитационного поля Земли, а не закон притяжения точечных масс, открытый Ньютоном. Правда, положение усложняется, если нужно принимать во внимание еще и влияние Луны.
Процедурные методы
11.4. Решение системы уравнений Вернемся вновь к системе уравнений, описывающих состояние множества из п материальных частиц с точечной массой. Если ограничиться учетом только самых главных силовых факторов, воздействующих на такую систему, то ее состояние описывается системой из 6п обычных дифференциальных уравнений в виде где и представляет массив из 6п компонентов позиций и скоростей п частиц, а g включает все внешние силы, действующие на частицы. Следовательно, если имеются две частицы а и Ь, связанные силами упругости без демпфирования, то получим иГ=["0 '<! «2 м3 М4 М5 иб М7 «8 и9 М10 "| I ]
= £ад а> а. ах а, а. Ьх £\ Ь. Ьх о\ Ь. ^
