р(и) = и7Мйр, где р есть матрица ансамбля опорных точек для формирования формы Безье. Ту же самую полиномиальную кривую можно представить и в виде р(м) = и7Л^, где М есть базисная матрица другой формы кривой, а q - матрица соответствующего ансамбля опорных точек. Если полиномы идентичны (речь ведь идет об изменении только формы представления кривой), то, приравняв правые части соотношений, получим Ч = М'Мйр.
В частности, для преобразования из формы интерполяционного полинома в форму Безье матрица пересчета должна иметь вид
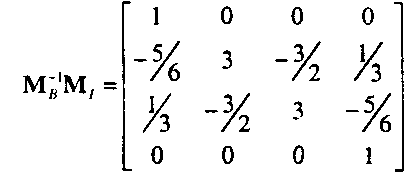
Для выполнения преобразования из формы кубического В-сплайна в форму Безье необходимо использовать матрицу пересчета в виде
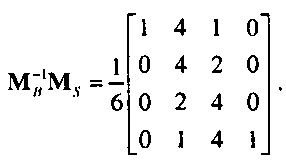
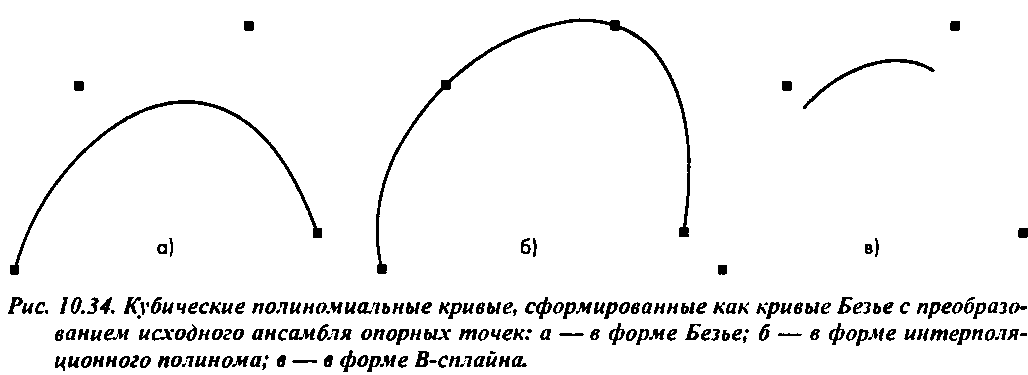
На рис. 10.34 показаны четыре опорные точки и построенные по ним кривые в форме Безье, в форме интерполяционного полинома и в форме В-сплайна. Все три кривые сформированы средствами построения кривых Безье, имеющимися в составе графической системы OpenGL. Интерполяционная кривая и В-сплайн сформированы как кривые Безье с использованием матриц пересчета МВ~]М{ и М/Г'Му. Обратите внимание на то, что кривая в форме В-сплайна сформирована только на интервале между двумя средними опорными точками исходного ансамбля.
Кривые и криволинейные поверхности
10.9.4. Разбиение поверхности Безье Описанный выше алгоритм разбиения можно распространить и на построение поверхностей в форме Безье. Порция поверхности Безье, представленная на рис. 10.35, сформирована по 16 опорным точкам. Каждые четыре точки в одном и том же столбце или строке задают сегмент кривой Безье, и, следовательно, к ним можно применить алгоритм разбиения. Но применительно к порции поверхности алгоритм должен разбивать ее не на две, а на четыре порции, поэтому модифицируем исходный алгоритм и преобразуем его в двухэтапный.
Сначала применим исходный вариант алгоритма к четырем сегментам, заданным шестнадцатью опорными точками, причем каждый сегмент соответствует определенному значению параметра и. В результате для значений и=0, 1/3, 2/3, 1 сформируются две группы по четыре опорные точки в каждой, причем средние точки будут принадлежать обеим группам. Таким образом, получим новые ансамбли по семь опорных точек вдоль каждого из четырех сегментов. На рис. 10.36 эти точки отмечены темными кружочками. Как видно на этом рисунке, все имеющиеся опорные точки (и прежние, и новые) можно разделить на три категории: исходные опорные точки, которые сохранились в новом ансамбле (они залиты серым цветом), новые опорные точки, которые появились в результате выполнения разбиения (они отмечены черными кружочками), и те точки исходного ансамбля, которые после разбиения отброшены (они отмечены белыми кружочками).
