После этого перейдем ко второму этапу. Выполним разбиение семи кривых, образованных новым ансамблем опорных точек, для семи фиксированных значений параметра г. Каждая кривая характеризуется четырьмя опорными точками, ко.^рые в результате применения алгоритма разбиения превращаются в семь (средняя точка используется совместно двумя новыми сегментами). Весь ансамбль опорных точек, образовавшийся после второго этапа выполнения алгоритма, показан на рис. 10.37. Разделив этот ансамбль на четыре группы по 16 точек в каждой (12 средних точек попадают в две группы, а одна- центральная - во все четыре), получим четыре новые порции поверхности Безье (рис. 10.38).

Рис. 10.35. Порция кубической поверхности Безье

Новые опорные точки, сформированные в результате разбиения О Исходные опорные точки, которые после разбиения отброшены

Исходные опорные точки, которые сохранились в новом ансамбле Рис. 10.36. Первый этап разбиения порции поверхности

10.9. Построение кривых и поверхностей

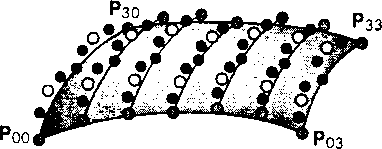
Новые опорные точки, сформированные в результате разбиения О Исходные опорные точки, которые после разбиения отброшены ® Исходные опорные тачки, которые сохранились в новом онсамбле Рис. 10.37. Опорные точки после второго этапа разбиения порции поверхности При выполнении такого двухэтапного алгоритма разбиения анализ "плоскостности" образовавшейся новой порции поверхности будет более сложным, чем при работе с кривой. Поэтому во многих системах разработчики просто фиксируют количество циклов разбиения, позволяя пользователю настраивать его программно. Если от системы требуется особо высокое качество построения образа поверхности на экране, разбиение выполняется до тех пор, пока размеры проекции порции поверхности на картинную плоскость не окажутся сравнимы с размерами пикселя.

10.10. Пример"opengl5_498.html">⇐ Предыдущая| |Следующая ⇒