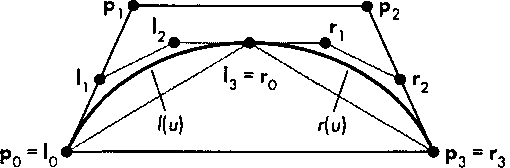
Рис. 10.32. Выпуклые оболочки и опорные точ ки кривой Безье и ее сегментов
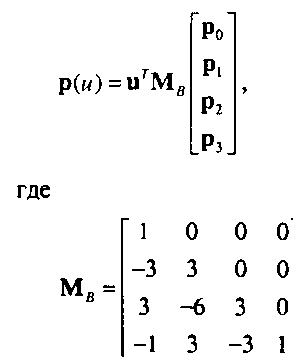
Кривые и криволинейные поверхности
Полином 1(м) должен проходить через точки р(0) и р( 1/2). Следовательно,
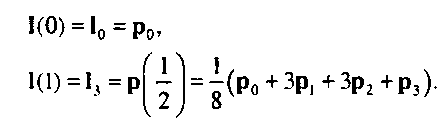
При м=0 касательная к I должна повторять касательную к р, но поскольку параметр и для кривой I имеет измененный масштаб по сравнению с параметром и~ кривой р, то, подставляя и~=2и, придем к выводу, что отношение между производными должно быть скорректировано с учетом соотношения (1и=2(1и. Следовательно, для производных в начальной точке сегмента справедливо соотношение Г(0)=3(11-10) = р'(0)=|(р1-Ро).
Рассуждая аналогично, выведем и соотношение для производных в средней точке р(и~) (она же последняя точка сегмента 1(и))"images/tmpB6CA-495.png">
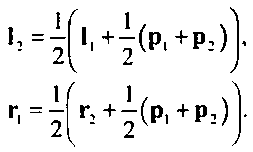
И, наконец, для точки сопряжения сегментов получим
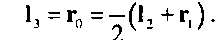
10.9. Построение кривых и поверхностей Преимущество такого метода определения опорных точек сегментов заключается в том, что он требует только операций суммирования и сдвига (для деления пополам), причем в единой процедуре определяются опорные точки обоих сегментов.
10.9.3. Построение других типов полиномиальных кривых методом разбиения Подобрав подходящий ансамбль опорных точек, любую полиномиальную кривую можно представить не только в форме Безье, но и в форме интерполяционного полинома, В-сплайна и т.д. Эффективность метода разбиения кривых Безье привела к тому, что обычно стараются любые кривые преобразовать в форму Безье. Алгоритмы преобразования можно сформулировать, анализируя процесс формирования кривой. Рассмотрим кубическую кривую в форме Безье. Ее можно описать следующим образом с помощью базисной матрицы Безье Мй:
