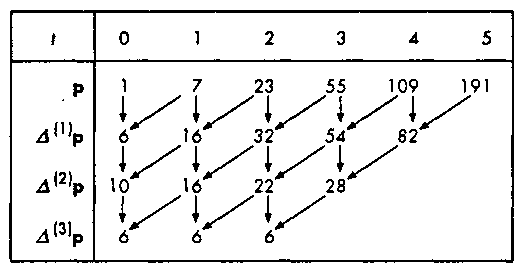
Рис. 10.30. Построение таблицы правых разностей
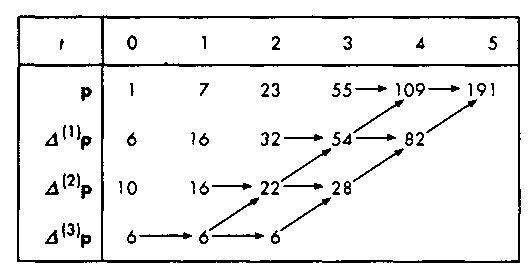
Рис. 10.31. Вычислительная схема, использующая таблицу правых разностей
10.9. Построение кривых и поверхностей
10.9.2. Рекурсивное разбиение кривых Безье Пожалуй, наибольшее распространение в компьютерной графике получил метод рекурсивного разбиения полиномиальных кривых Безье. В основе метода лежит использование выпуклой многоугольной оболочки, причем в процессе вычислений по этому методу никогда не приходится в явном виде вычислять значения полиномов. Пусть имеется описание кубической кривой Безье (метод пригоден и для обработки кривых Безье более высокой степени). Известно, что кривая должна быть расположена в области, ограниченной выпуклой многоугольной оболочкой, построенной на опорных точках, как на вершинах. Разделим кривую на два сегмента 1(и) и г(н). Каждый сегмент имеет область определения, равную половине исходного интервала. Поскольку исходная кривая кубическая, то и каждый из сегментов является кубической кривой. Учтите, что поскольку каждый сегмент имеет область определения, равную половине исходного интервала, то придется изменить масштаб представления параметра и для 1 и г таким образом, чтобы на каждом сегменте и изменялся в диапазоне (0, 1). Сегмент \(и) представляет левую половину р(м), а сегмент г(и)- правую. Каждый из сегментов имеет четыре опорные точки, которые, во-первых, определяют его форму, а во-вторых, служат вершинами выпуклой многоугольной оболочки. Обозначим эти два множества опорных точек {10,1ь 12, Ь} и {г0, гь г2, г3}. Исходная кривая р(и) имеет ансамбль опорных точек {р0, рь р2, Рз}- Все три ансамбля и кривая р(и), разбитая на сегменты \(и) и г(и), показаны на рис. 10.32. Обратите внимание на то, что выпуклые оболочки для 1 и г всегда будут лежать внутри выпуклой оболочки для р, что является следствием из свойства уменьшения вариации (variation-diminishing property), которым обладают кривые Безье.
Рассмотрим левый сегмент. Можно выяснить, насколько многоугольник оболочки является выпуклым, измерив расстояние между точками 1, и 12 и отрезком, связывающим 10 и 13. Если расстояние не превышает некоторой наперед заданной величины, то вместо криволинейного сегмента 1(и) можно провести прямую. В противном случае можно разделить сегмент 1(и) еще на пару сегментов и проанализировать их выпуклость. В результате получилась рекурсивная процедура, которая на первый взгляд не требует вычисления значений полинома. Но у читателей, естественно, должен возникнуть вопрос, а откуда мы возьмем данные о положении опорных точек (10, Ii, 12, Ь} и {г0, гь г2, г3} сегментов кривой после разбиения, которые одновременно являются и вершинами многоугольных выпуклых оболочек этих сегментов. Ниже будет показано, как отыскать эти вершины для левого сегмента 1(г/), а процедура для правого сегмента будет симметричной (в смысле индексов точек). Начнем с представления кривой Безье, знакомого нам по разделу 10.6.1"opengl5_495.html">⇐ Предыдущая| |Следующая ⇒
