Нули этих четырех полиномов расположены вне интервала [0, 1], а потому функции смешивания являются гораздо более гладкими, чем для интерполяционных полиномов (см. упр. 10.16).
Воспользовавшись представленными выше функциями смешивания, можно следующим образом определить порцию поверхности в форме Эрмита: Р(и,*) = Х5>((и)*;(у)Ч(/,
1=0 у=0
где 0=[я7/] - набор данных, представляющих порцию поверхности аналогично тому, как q представляет сегмент кривой. Но пока что эти уравнения являются для нас чисто формальными выражениями. Совершенно неясно, как связаны между собой элементы и производные функции р(«, V). Четыре элемента О представляют собой значения функции р(и, у) в угловых точках порции поверхности, а четыре других должны представлять производные к поверхности в этих угловых точках. В интерактивных приложениях пользователю желательно специфицировать не данные о производных, а координаты точек, и, следовательно, не сформулировав аналитические выражения для этих данных, мы не сможем получить производные.
10.5. Эрмитова форма представления кривых и поверхностей
10.5.2. Геометрическая и параметрическая непрерывность
Перед тем как мы перейдем к обсуждению форм представления Безье и сплайнов, кратко рассмотрим проблему непрерывности представления и его производных в общем виде. На рис. 10.14 показаны два последовательных сегмента составной параметрической кривой. Обозначим полином левого сегмента р(м), а полином правого - q(w) Сформулируем разные условия непрерывности, сопоставляя значения полиномов и их производных в точке сопряжения и=\ для р(и) и и=0 для q(и). Если желательно, чтобы составная кривая была непрерывной, необходимо в точке сопряжения обеспечить выполнение условия
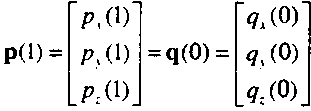
В точке сопряжения значения всех трех параметрических компонент векторов р и q должны быть равны. Кривые, в которых такие условия удовлетворяются, назовем кривыми, обладающими параметрической непрерывностью (parametric continuity) класса С0.
Переходя к анализу производных в точке сопряжения, можно сформулировать условие непрерывности по первой производной аналогично тому, как это делалось при обсуждении формы Эрмита:
