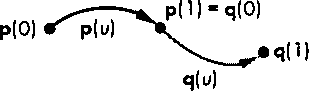
Рис. 10.14. Непрерывность составной кривой в точке сопряжения
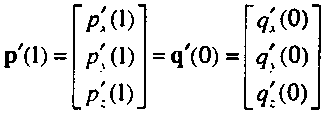
Кривые, в которых условия непрерывности удовлетворяются и для значения, и для первой производной, назовем кривыми, обладающими параметрической непрерывностью класса С1.
Теперь взглянем на проблему непрерывности с точки зрения геометрии. Производная к кривой, заданной параметрически, в некоторой точке есть вектор касательной к этой кривой, направленный в сторону увеличения значения параметра. Предположим, что в точке сопряжения вместо равенства значений компонент производной к сегментам мы потребуем только соблюдения пропорциональности этих компонент
Р'(1) = *Ч'(0), с некоторым коэффициентом к. Если касательные к обоим сегментам пропорциональны, то соответствующие векторы параллельны (имеют одинаковое направление), но имеют разную длину. Будем говорить, что составная кривая, удовлетворяющая этим условиям, обладает геометрической непрерывностью (geometric continuity) класса8 С71. Если необходимо, чтобы касательные к сегментам в точке сопряжения были только пропорциональны, то от нас требуется соблюдение двух условий вместо трех. В результате появляется "лишняя" степень свободы, которую можно использовать для удовлетворения других условий. Эту идею можно распространить и на производные высших порядков, т.е. рассматривать классы параметрической непрерывности С" и геометрической непрерывности G".
Отметим, что форма кривой, обладающей геометрической непрерывностью класса G\ зависит от коэффициента пропорциональности длин касательных к сегментам в точке сопряжения. На рис. 10.15 показано, что форма сегментов кривых, совпадающих в конечных точках и имеющих в этих точках пропорциональные векторы касательных, довольно существенно от вКласс в0 геометрической непрерывности предусматривает выполнение тех же условий, что и класс С0 параметрической непрерывности.
Кривые и криволинейные поверхности
личается. Это свойство часто используется в графических программах вычерчивания, в которых пользователю предоставляется возможность регулировать значение коэффициента про порциональности векторов касательных и таким способом настраивать желаемую форму вычерчиваемой кривой. В других приложениях, в частности связанных с анимацией, составные кривые задают траекторию движения объектов, и в таком случае геометрическая непрерывность класса С1 оказывается явно недостаточной (см. упр. 10.11).
