10.5.1. Форма Эрмита В этом разделе будет рассмотрена форма представления кривых, предложенная Эрмитом (Hermite). Предположим, что анализ сегмента кривой мы начинаем, имея в своем распоряжении только точки7 ро и р3, и что по-прежнему сегменту соответствует интервал изменения параметра [0, 1], т.е. имеющиеся точки соответствуют значениям параметра и=0 и и=\. Используя те же обозначения, что и раньше, можно записать два условия: Р(0) = Ро = с0, р(1) = р3 = Со+С,+С2+Сз.
Два других условия получим, зная значения производных функции в крайних точках сегмента и=0 и и=\. Производная кубического полинома есть квадратный полином
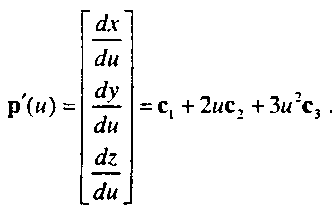
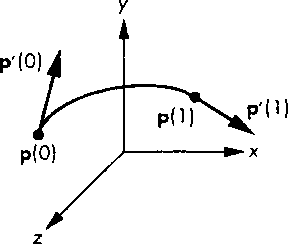
Обозначим известные значения производных в конечных точках р'0 и р'3. Тогда два дополнительных условия примут вид (рис. 10.12)
р'о = р'(0) = с,, р,з = р,(1) = с,+2с2+3с3.
Эти же уравнения можно записать и в матричной форме: Рис. 10.12. К определению формы Эрмита для кубической кривой
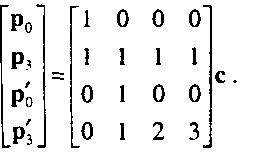
7Для единообразия мы здесь используем принятую ранее нумерацию опорных точек. Эта же нумерация будет использоваться и при анализе кривых Безье в разделе 10.6.
432 Глава 10. Кривые и криволинейные поверхности Обозначив через q матрицу имеющихся в нашем распоряжении данных
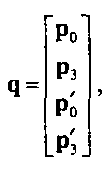
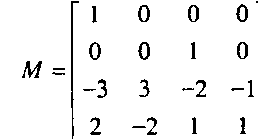
можно записать решение уравнения в виде c = M„q, где Мя называется базисной матрицей Эрмита (Hermite geometry matrix): В результате получим представление полиномиальной кривой в форме Эрмита: р(м) = итМн<\.
Мы будем использовать форму Эрмита для представления сегментов составной кривой, как показано на рис. 10.13. Точка сопряжения является общей для обоих сегментов, и, кроме того, производные к кривой в точке сопряжения для обоих сегментов также равны. В результате получаем составную кривую, непрерывную по первой производной на всем протяжении.
Возможность получения более гладких кривых при использовании формы представления по Эрмиту можно обосновать математически следующим образом. Запишем полином в виде р(м) = Ци)тц, где новые функции смешивания имеют вид
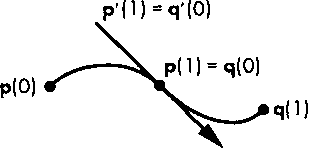
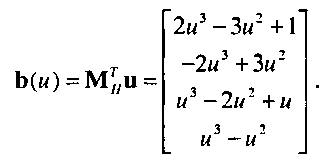
Рис. 10.13. Применение формы представления по Эрмиту к стыковке сегментов
