10.4.2. Порция кубической интерполяционной поверхности Все, что было сказано о сегментах интерполяционных кривых, можно достаточно просто распространить и на трехмерный случай порции интерполяционной поверхности. Бикубическое уравнение порции поверхности можно записать в следующем виде:
3 3Р(и.у) = £Хм'уЧ •
Здесь С// - трехкомпонентная матрица-столбец, элементами которой являются коэффициенты при одинаковых степенях независимой переменной в уравнениях для х, у и г компонент. Определим 4х4-матрицу таким образом, что ее элементами будут трехкомпонентные матрицы-столбцы: С = [с„].
Тогда описать порцию поверхности можно следующим образом: р(м, V) = ц7Су, где
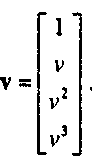
Конкретная порция бикубической поверхности определяется 48 значениями элементов матрицы С - 16-ю трехмерными векторами.
Допустим, что имеется 16 трехмерных опорных точек р(/, /-0,..,3,/=О,..,3. Эти точки можно использовать для определения порции интерполяционной поверхности (рис. 10.11). Будем считать, что эти данные используются для интерполирования с равным шагом по обоим Глава 10. Кривые и криволинейные поверхности независимым параметрам и и v, которые принимают значения 0, 1/3, 2/3 и 1. Отсюда получим три набора из 16 уравнений с 16 неизвестными в каждом. Например, при !/=у=0 получим три независимых уравнения:
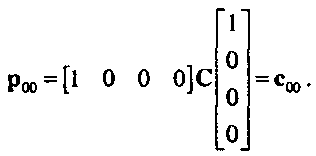
Мы не будем выписывать и решать эти уравнения, а поступим проще. Если зафиксировать у=0, то, изменяя м, получим кривую, проходящую через роо, р)у, Рго» р30. Используя результаты, полученные в предыдущем разделе, можем записать для этой кривой следующее соотношение:
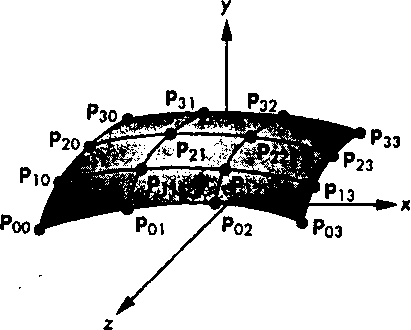
Рис. 10. П. Порция интерполяционной поверхности
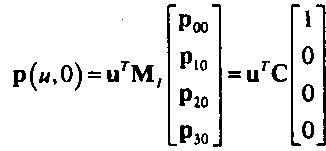
При значениях v=l/3, 2/3, 1 можно определить три другие интерполяционные кривые, каждую из которых можно описать тем же способом. Объединив уравнения для всех кривых, получим интересующую нас систему из 16 уравнений:
u7M,P = urCAr,где А - матрица, обратная М,. Решением этого уравнения будет искомая матрица коэффициентов: С = М/РМ/.
Подставляя ее в уравнение поверхности, окончательно получим p(w, v) - u7'M/PM/v.
