10.4.1. Функции смешивания Можно иначе подойти к анализу гладкости интерполяционных полиномиальных кривых. Перепишем выведенные в предыдущем разделе соотношения в слегка измененном виде. Подставив коэффициенты интерполяции в полином, получим р(м)=и'с=и7М/р.
Это соотношение можно записать в виде р(и) = Ъ(и) 'р, где
Ь(м) = М/и есть матрица-столбец из четырех полиномиальных функций смешивания (blending polynomials):
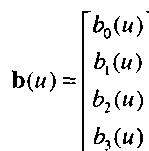
В каждой функции смешивания полином является кубическим. Выразив р(г<) как сумму полиномов смешивания, получим ч
р(и) = Ь0(и)р0+Ь1(и)р) + Ь2(и)р2+Ь,(и)р3 = ^Ь,(и)р, .
1=0Из этого соотношения следует, что полиномиальные функции смешивания характеризуют вклад, который "вносит" каждая опорная точка, и таким образом позволяют оценить, насколько скажется на виде конечной кривой изменение положения той или иной опорной точки5. Графики функций смешивания для кубического интерполяционного полинома показаны на рис. 10.10, а соответствующие аналитические выражения приведены ниже:
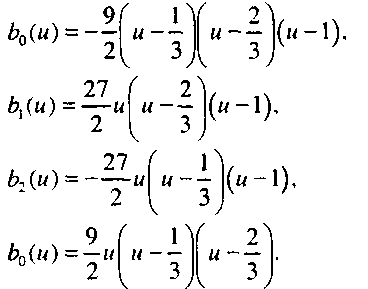
Поскольку все нули функций смешивания лежат в интервале [0, 1], то их значения могут существенно изменяться на этом интервале, а сами функции не являются монотонными. Эти характеристики функций смешивания следуют из того факта, что интерполяционная кривая должВ литературе по отношению к тем функциям, которые мы назвали функциями смешивания, иногда используется и другой термин - "полиномиатьные весовые функции при опорных точках". - Прим. ред.
10.4. Интерполяция на точно проходить через опорные точки, а не в ближайшей их окрестности. Еще более характерны такие особенности для интерполяционных полиномиальных кривых порядков выше четвертого. Плохая гладкость кривой, а также отсутствие непрерывности производных в точках сопряжения сегментов и объясняют, почему интерполяционные полиномиальные кривые редко используются в компьютерной графике. Но пользуясь той же методикой анализа, можно отыскать и тип представления кубической кривой, более подходящий для наших задач.
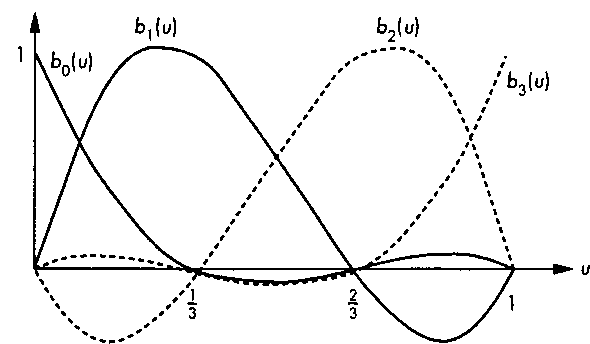
Рис. 10.10. Полиномиальные функции смешивания для случая кубической интерполяции
