J 0.4. Интерполяция
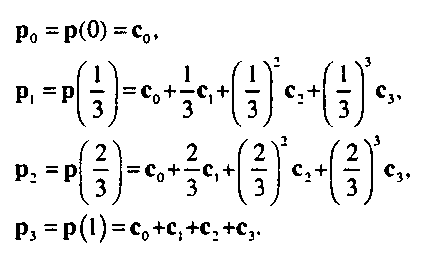
Перепишем эти уравнения в матричной форме следующим образом: р = Ас,
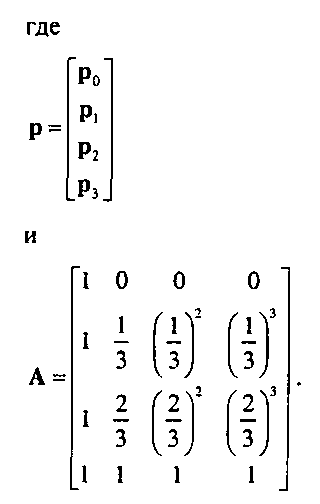
Проанализируем матрицу А. Если интерпретировать рис как матрицы-столбцы из 12 элементов, то правило умножения матриц соблюдено не будет. Но мы можем и по-другому интерпретировать матрицы рис - рассматривать их как матрицы-столбцы из четырех элементов, каждый из которых, в свою очередь, является матрицей-строкой. Тогда умножение элемента матрицы А, скаляра, на элемент матрицы с, трехмерную матрицу-строку, даст в результате трехмерную матрицу-строку, т.е. элемент того же вида, что и элементы матрицы-столбца р. Можно показать, что матрица А не является вырожденной и, следовательно, ее можно обратить и получить базисную интерполяционную матрицу (interpolating geometry matrix):
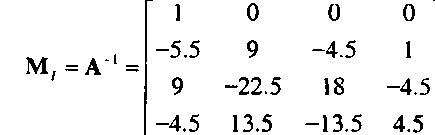
Располагая значениями элементов М/, можно вычислить искомые значения коэффициентов: с = М/р.
Теперь предположим, что кривая задана не четырьмя, а т опорными точками р0, р1}.., рш. Такую кривую можно представить интерполяционным полиномом (т~\)-го порядка и, используя описанную выше методику, вычислить Зх/я коэффициентов с,7 (/=0,..,/н-1; у'=.г, у, г).
Но можно поступить и по-другому - считать эту кривую состоящей из нескольких сегментов, каждый из которых является кубической кривой и задается очередной группой из четырех опорных точек. Непрерывность кривой можно обеспечить тем, что считать последнюю опорную точку предшествующей группы (последнюю точку сегмента) первой опорной точкой следующей группы (первой точкой очередного сегмента) (рис. 10.9). Следовательно, для формирования первого сегмента будут использованы опорные точки р0. Рь р2, Рз, Для формирования второго - точки р3, р4, р5, р6 и т.д. Обращаю ваше внимание на то, что если
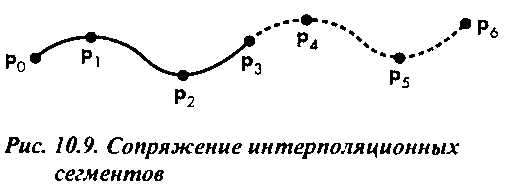
Кривые и криволинейные поверхности
на каждом сегменте полагается, что параметр и изменяется в интервале [0, 1], то матрицы М/ для всех сегментов одинаковы. Хотя таким способом мы и получим непрерывную кривую, функции производных по параметру будут претерпевать разрывы в точках сопряжения.
