4В дословном переводе surface patch - лоскут поверхности. - Прим. перев.
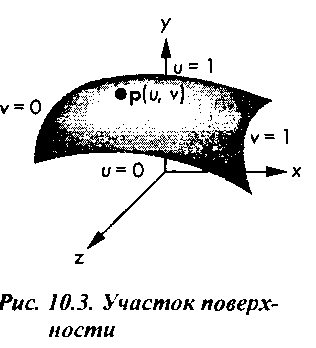
Кривые и криволинейные поверхности
приходится уделять больше всего внимания при выборе способа аппроксимации. На рис. 10.7 показана непрерывная линия, первая производная которой не является гладкой функцией, - претерпевает разрыв в точке сопряжения. Общепринятое определение гладкости кривой связано с характеристиками функций первой производной по параметру и производных более высоких порядков. Для нас представляют интерес гладкие кривые, т.е. такие, функция первой производной которых непрерывна на всем интервале существования параметра. В некоторых случаях гладкой должна быть не только функция первой производной, но и производных более высокого порядка. Эти определения станут более понятны для вас после изучения материала раздела 10.3. Сейчас же отмечу, что для полиномиальной кривой все производные до п-го порядка включительно являются гладкими и могут быть определены аналитически. Следовательно, единственное место, где могут возникать разрывы при аппроксимации произвольной гладкой кривой сегментами полиномиальных кривых - это точки сопряжения.
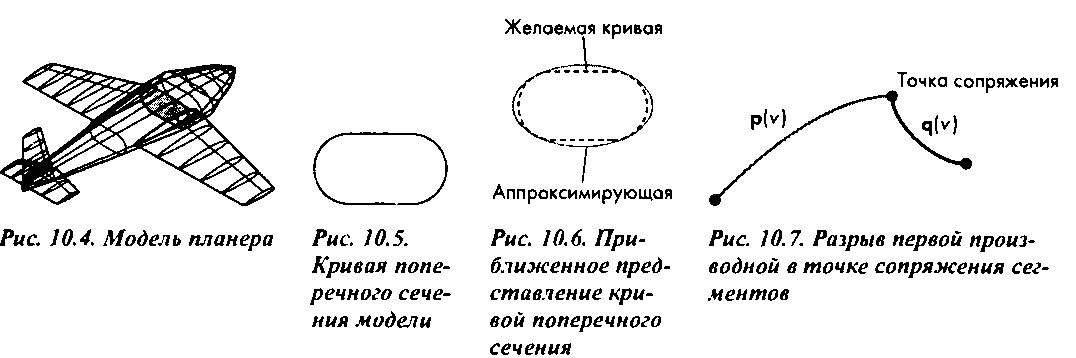
Процесс формировании кривой желательно организовать таким образом, чтобы каждый сегмент строился индивидуально, а не строить все сегменты единой глобальной вычислительной процедурой. Причина, но которой такая организация предпочтительнее, заключается в том, что в таком режиме пользователю гораздо удобнее подбирать форму кривой на отдельных участках, следуя специфическим требованиям приложения. Внесение небольших изменений в спецификацию кривой приводит только к локальным изменениям ее формы на том участке, с которым в текущий момент работает пользователь, и мало влияет на остальные участки. Такой способ реализует устойчивую стратегию конструирования, которая неформально может быть охарактеризована следующим образом: малые вариации исходных параметров на входе должны приводить к малым вариациям результата на выходе.
Работая с деревянными рейками, желательно иметь возможность гнуть их таким образом, чтобы как можно точнее воспроизвести желаемую форму шпангоута. Более того, желательно свести всю процедуру к выбору небольшого ансамбля опорных или контрольных точек (control points), которые будут полностью характеризовать форму сегмента кривой. На рис. 10.8 показан сегмент
