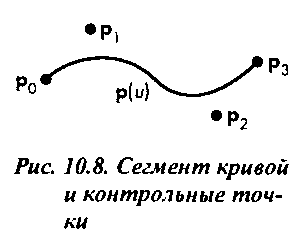
кривой и ансамбль описывающих его контрольных точек. Обратите внимание на то, что через некоторые контрольные точки сегмент проходит, а некоторые располагаются вблизи действительной кривой. Как будет показано ниже, во многих задачах компьютерной графики и автоматизации проектирования нас вполне устраивает, если кривая проходит в малой окрестности заданных контрольных точек и при этом обеспечивается ее гладкость.
10.2. Общая характеристика полиномиальной параметрической формы.
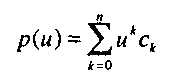
Этот пример наглядно демонстрирует, почему в задачах компьютерной графики предпочтение отдается классу полиномиальных кривых. Даже наименование класса составных полиномиальных кривых- сплайн-кривые, или стайны- произошло от английского наименования гибкой деревянной рейки или упругой стальной ленты, с помощью которой в кораблестроении вычерчивались гладкие контуры. Такая лента вставлялась между штифтами, соответствующими положению контрольных точек на кривой, и за счет упругости образовывала гладкую линию контура. Оказалось, что эта линия математически описывается сегментами полиномиальных кривых степени не выше третьей. За такими составными полиномиальными кривыми и закрепилось название сплайнов. Сплайны мы подробно рассмотрим в разделах 10.7 и 10.8.
Возвращаясь к задачам компьютерной графики, напомню, что помимо собственно математического описания кривых, нам понадобится разработать и методы их отображения. Математический аппарат, даже очень изящный, останется "вещью в себе", если мы не сможем им воспользоваться для представления на экране кривых и поверхностей. Нам необходимы такие способы отображения криволинейных объектов, которые не превосходили бы по сложности аналогичные методы, которыми мы пользуемся для отображения прямолинейных и плоских объектов, и обладали теми же функциональными возможностями - раскрашивать и тонировать объекты, накладывать на них текстуры разного вида.
10.3. Параметрически заданные кубические кривые Остановившись на классе полиномиальных кривых в параметрической форме, мы должны выбрать степень полинома для описания кривой. Если воспользоваться полиномом очень высокой степени, то при конструировании кривой определенной формы у нас будут в значительной степени "развязаны руки", поскольку в нашем распоряжении будет больше коэффициентов, но процесс расчета координат точек на кривой потребует большего количества вычислений. Кроме того, при работе с полиномами высоких степеней возрастает опасность получить кривую волнистой формы. С другой стороны, выбор полинома слишком низкой степени может привести к тому, что в нашем распоряжении окажется слишком мало регулируемых параметров - коэффициентов полинома - и, следовательно, не удастся воспроизвести с требуемой точностью форму кривой. Выход можно найти в том, чтобы не описывать единым полиномом высокой степени всю кривую, а разбить ее на сегменты небольшой длины, которые можно описывать полиномами низкой степени. Хотя такой полином и обладает малым, количеством степеней свободы, их может оказаться вполне достаточно, чтобы воспроизвести форму кривой на отрезке небольшой длины. Основываясь на этих достаточно общих рассуждениях, многие конструкторы, не мудрствуя лукаво, приступая к формированию кривых, начинают с кубического полинома- начинать с квадратичной формы, если на то заранее нет веских оснований, все-таки несерьезно, а сразу браться за полином четвертой степени боязно, а вдруг третьей степени вполне хватит.
