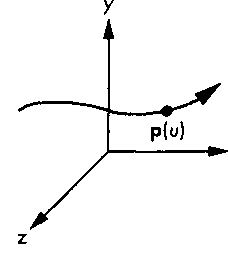
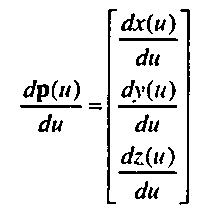
Рис. 10.1. Кривая, заданная в параметрической форме можно рассматривать как вектор скорости обхода кривой, который в каждой точке этой кривой направлен по касательной к ней.
Для описания поверхности в параметрической форме требуется использовать два параметра. Система уравнений поверхности имеет вид х = х(и, V), У = У(и. V), 2 = 2(и, V).
Эти же уравнения можно записать в виде матрицы-столбца р(и, у)=[дс(м, V) у(и, у) г(м, у)]Т. Изменяя значения параметров и и V в некотором интервале, можно сформировать значения координат р(м, V) всех точек поверхности. При анализе примера сферической поверхности в главе 6 мы уже отмечали, что матрицы-столбцы Эр/Эй и Эр/Эу описывают плоскости, касательные к поверхности в каждой ее точке.
Параметрическая форма описания кривых и поверхностей является, во-первых, наиболее гибкой, а во-вторых, устойчивой к любым вариациям формы и ориентации объектов, что делает ее особенно удобной для использования в математическом обеспечении систем компьютерной графики. Возможно, у кого-либо из читателей появится возражение, что и в этой форме мы привязаны к системе координат х, у, г, но это не так. Можно модифицировать параметрические уравнения и использовать для описания кривой в трехмерном пространстве только касательные и нормали, которые образуют так называемый сопровождающий трехгранник (трехгранник Френе), имеющий отличную ориентацию в каждой точке кривой. Что касается задач компьютерной графики, то использование параметрической формы представления координат х, у, г вполне удовлетворяет все их потребности.
Кривые и криволинейные поверхности
10.1.4. Параметрические полиномиальные кривые Параметрическая форма представления определенной кривой или поверхности не является уникальной. Объект можно представить множеством способов, но мы сосредоточим внимание на полиномиальной форме, т.е. все функции параметра и при описании кривых или параметров и и г при описании поверхностей являются полиномами. Эта форма чаше всего используется в компьютерной графике, а ее достоинства будут проанализированы в разделе 10.2.
