Рассмотрим уравнения кривой в виде"
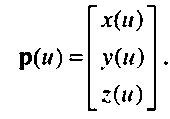
Полиномиальная параметрическая кривая степени п имеет вид где с* имеет независимые компоненты х, у, 2, т.е.
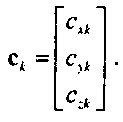
Матрица {с*}, состоящая из п+\ столбцов, объединяет коэффициенты полиномов для компонентов р; это означает, что у нас есть 3(л+1) степеней свободы в выборе коэффициентов для конкретной кривой р. Уравнения для трех компонентов х, у, 2 независимы и каждое из них имеет вид а следовательно, обладает п+\ степенью свободы. Кривую можно определить на любом интервале изменения параметра и итт <и< мтах, но, не теряя общности рассуждений, можно положить, что 0 < и < 1 (см. упр. 10.3). По мере того как параметр и будет "пробегать" значения в этом интервале, отображающая точка будет перемещаться по сегменту кривой (рис. 10.2).
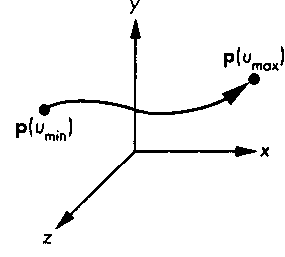
Рис. 10.2. Сегмент кривой
10.1.5. Параметрические полиномиальные поверхности Параметрическая полиномиальная поверхность описывается уравнением вида
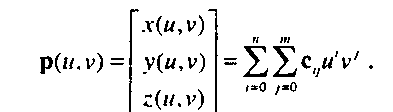
2При изложении этого материала мы не будем пользоваться аппаратом однородных координат. Об использовании этого аппарата мы поговорим в разделе 10.8, когда будем обсуждать кривые в форме рациональных В-сплайнов на неравномерной сетке (NURBS-cn.naUHoe).
3В OpenGL часто используется термин "порядок" полинома (oxàcx), который имеет значение на 1 большее, чем степень полинома.
10.1. Представление кривых линий и поверхностей Таким образом, для определения конкретной поверхности р(г/, v) необходимо задать 3(п+\)(т+\) коэффициентов. Можно при анализе положить п=т, а параметры и и v изменять на интервале 0 < и, v < 1 и таким образом определить порцию поверхности (surface patch4), как показано на рис. 10.3. Обращаю ваше внимание на то, что определенный таким способом участок поверхности можно рассматривать как предел, к которому стремится множество кривых, которые формируются, когда один из параметров и или v пробегает значения в своем интервале, в то время как другой сохраняет постоянное значение. В дальнейшем при обсуждении поверхностей будет использована следующая стратегия"opengl5_470.html">⇐ Предыдущая| |Следующая ⇒
