9.9. Дискретизация изображения функция одной переменной и выборки на ней, а на рис. 9.40,6 - ограниченный спектр этой непрерывной функции. На рис. 9.40,в вы видите спектр решетчатой функции, который повторяет в каждом периоде спектр исходной непрерывной функции. Поскольку частота квантования при построении решетчатой функции была выбрана выше частоты Найквиста, между периодами в спектре решетчатой функции отчетливо видны участки с нулевой интенсивностью.
А теперь рассмотрим случай, представленный на рис. 9.41. В нем критерий Найквиста нарушен, а потому копии фурье-образа исходной функции в спектре решетчатой функции перекрываются. Центральная часть этого графика в увеличенном масштабе показана на рис. 9.42. На нем вы видите копию фурье-образа исходной непрерывной функции, построенную в начале координат частотной области, и первую правую от нее копию, сдвинутую на период частоты квантования Частота £о выше частоты Найквиста bJ2. В точке ^s-^o, которая ниже частоты Найквиста, на составляющую центральной копии накладывается составляющая Ь$ правой копии. Если исходная функция представляет звуковые колебания, то в квантованном сигнале мы услышим усиление мощности звука на этой частоте. Точно так же, если сигнал с подобными характеристиками (но уже двухмерный) представляет изображение, то на экране будут заметны искажения формы картинки. Мы говорим, что в квантованном сигнале частота £о имеет побочную реплику (alias) на частоте ^-^о. Обращаю ваше внимание на то, что при появлении побочной реплики ее нельзя отличить от составляющей основной копии фурье-образа исходной функции, т.е. информация, которую несет эта частота в исходном сигнале, будет искажена побочной репликой.
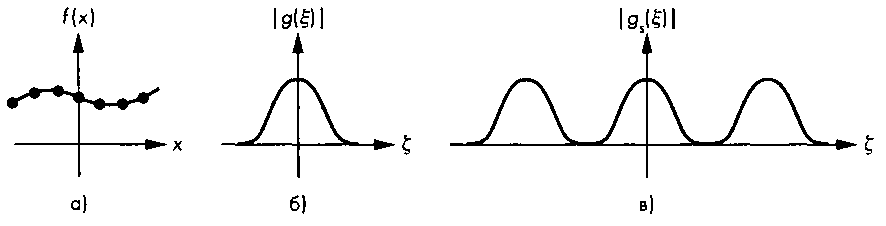
Рис. 9.40. Функция с ограниченным спектром: а - функция и выборки на ней в пространственной области; б - спектр непрерывной функции; в - спектр решетчатой функции
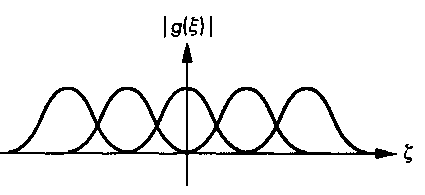
Рис 9.41. Перекрытие фурье-образов исходной функции в спектре решетчатой функции
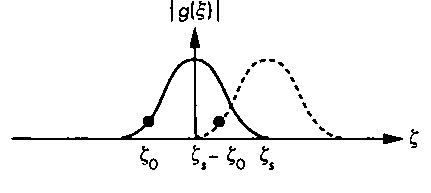
Рис. 9.42. Появление побочной низкочастотной составляющей в спектре решетчатой функции
