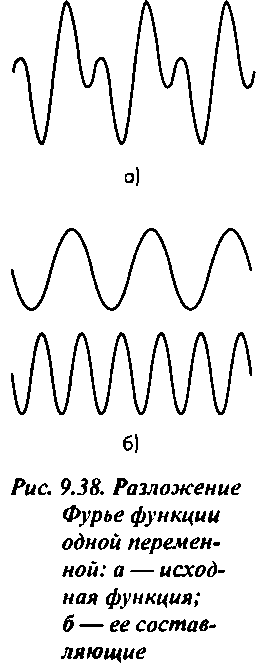
Для математического анализа процесса квантования используется аппарат преобразования Фурье. Суть его состоит в том, что любая функция (не имеет значения, задана она в пространственной или во временной области) может быть представлена в виде суммы ряда, возможно, бесконечного, элементами которого являются синусоиды с разной частотой. Эта концепция легко интерпретируется в отношении звуковых сигналов в терминах спектра такого сигнала. Когда речь идет о двухмерной функции изображения, составляющие Фурье имеют вид пространственных синусоид с кратными частотами. На рис. 9.38,а показан одномерный периодический сигнал сложной формы, а на рис. 9.38,6 - две его спектральные составляющие. На рис. 9.39 показаны две пространственные синусоиды - периодические функции двух переменных. Как следует из теории Фурье, любая двухмерная пространственная функция имеет две эквивалентные формы представления - в пространственной области J(x, у)нв частотной области g(£, т|). Значения функции g - это "взнос" периодической функции с частотами (£, т]) в пространственный спектр изображения. Использование представления изображения в частотной области позволяет проанализировать многие его свойства, в том числе и те, которые сказываются на результатах квантования по пространству.
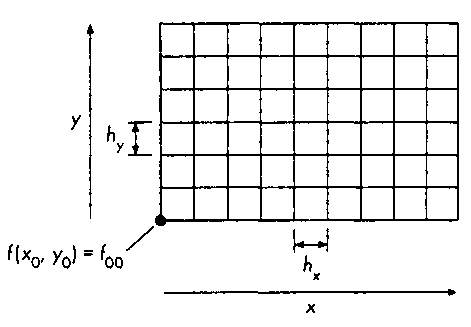
Рис. 9.37. Квантование изображения по пространству
Операции с изображением на уровне растрового представления
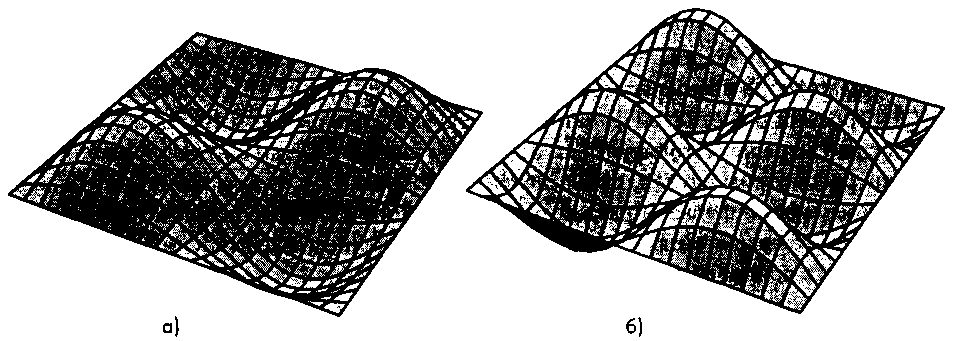
Рис 9.39. Периодические функции двух переменных
Постараемся пояснить суть процесса квантования, не прибегая к сложным математическим выкладкам. Теория дискретизации изображения базируется на теореме Найквиста о выборках (Nyquist sampling theorem). Эта теорема состоит из двух частей, первую из которых мы будем использовать при анализе погрешностей квантования, а вторую - при анализе восстановления непрерывного изображения по дискретным выборкам.
Теорема Найквиста о выборках (часть 1). Ансамбль идеальных выборок непрерывной функции содержит всю информацию об исходной функции тогда и только тогда, когда частота квантования как минимум вдвое превышает максимальную частоту в спектре исходной функции6.
