матрицу преобразований в однородных координатах, задающую отношение в пространстве между объектом данного узла (и всеми объектами его дочерних узлов) и объектом его родительского узла;
указатель на дочерний узел.
В структуру узла можно включать и другую информацию, например набор атрибутов (цвет, трафарет заполнения, свойства материала и т.п.). Формирование изображения модели, описанной такой иерархической структурой данных, требует обхода дерева (tree traversal)- нужно "посетить" каждый узел и при обработке каждого узла вычислить элементы матрицы, которая Рис 8.11. Представление узла структурой данных в программе
8.3. Модель руки робота будет определять преобразования примитивов, описывающих соответствующий графический объект, и затем уже сформировать их изображения. В той программе, которую мы рассмотрели выше, такой обход был реализован неявно.
Рассмотренный пример довольно прост - каждый узел в нем имеет только один дочерний. В следующем примере мы встретимся с более сложной иерархией объектов.
8.4. Обход деревьев На рис. 8.12 показана фигура киборга - персонажа множества комиксов. Если выбрать корпус киборга в качестве объекта корневого узла иерархии, то всю фигуру можно представить деревом, показанным на рис. 8.13. После того как положение корпуса будет задано, положение и ориентацию его конечностей можно определить углами поворота в соответствующих сочленениях. Можно "оживить" в программе фигуру киборга, изменяя значения углов в сочленениях. В этой простейшей модели в коленях и локтях имеются сочленения с одной степенью свободы, но можно создать и более сложную модель, поместив сочленения с двумя степенями свободы. А в сочленении, моделирующем шею, можно и в этом простом варианте определить две степени свободы.
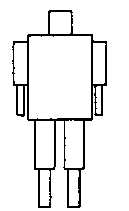
Рис. 8.12. Фигурка киборга
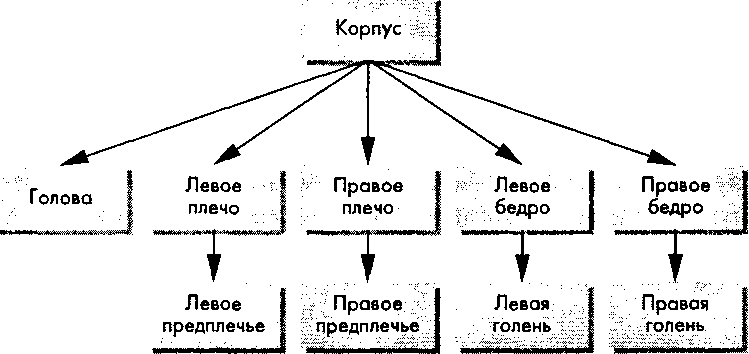
Рис. 8.13. Представление фигурки киборга в виде дерева Предположим, что разработано несколько функций вроде Ьеас1() или 1е£г,_иррег_агт(), которые формируют изображения отдельных компонентов фигурки (символов) в собственных системах координат. Далее можно сформировать набор описаний узлов дерева определить в них матрицы преобразования символа, с которым связан узел, относительно символа родительского узла, точно так, как мы это делали при построении иерархии звеньев робота в предыдущем разделе. Будем считать, что каждый символ описан таким образом, что не требуется изменять его масштаб. Тогда матрицы преобразований в узлах будут включать произведение только матриц сдвига и поворота. На схеме дерева соответствующие матрицы можно использовать для маркировки ребер, как это показано на рис. 8.143. Не забывайте, что каждая матрица представляет преобразование относительно предыдущего узла и что для получения преобразования относительно мирового фрейма нужно перемножить матрицы по пути обхода графа.
