Закрашивание
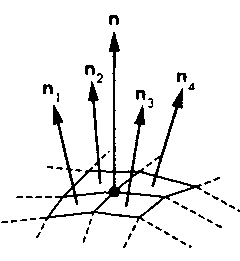
кающихся в этой вершине. Для примера, представленного на рис. 6.30, с выделенной вершиной ассоциируется нормаль, вычисленная в соответствии с соотношением
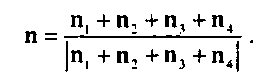
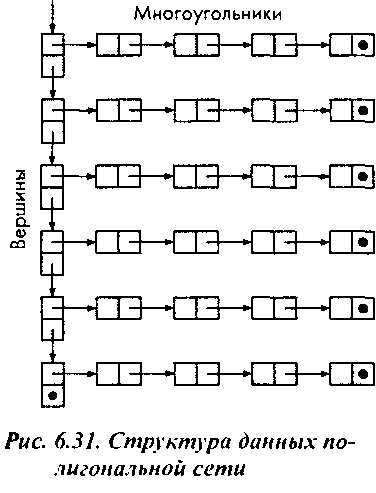
Метод Гуро довольно просто реализуется в программе, использующей OpenGL. От прикладного программиста требуется только правильно вычислить нормали, ассоциируемые с вершинами полигональной сети. В литературе часто смешиваются метод закрашивания Гуро и интерполяционный метод закрашивания. Иногда это вызывает определенные проблемы. Как определить, какие нормали следует усреднять для вычисления нормали, ассоциируемой с определенной вершиной? Если структура данных в программе линейна, т.е. все вершины перечислены в обычном линейном списке, мы не располагаем информацией о том, какие именно многоугольники пересекаются в определенной вершине. Сам собой напрашивается вывод, что требуется такая структура данных, которая отражала бы связи между многоугольниками в сети. Просматривая такую структуру данных, можно определить те вершины, в которых следует усреднять векторы нормалей. Такого рода структура данных должна связывать, как минимум, многоугольники, вершины и свойства материалов. Один из возможных вариантов ее организации представлен схематически на рис. 6.31. Нас в ней интересует информация о том, какие именно многоугольники пересекаются в каждой вершине.
Пример изображения со сглаженным закрашиванием представлен на ил. 6 цветной вклейки. Этот цветовой куб уже использовался в примерах, описанных в главах 2 и 3. Текст программы формирования этого куба читатель найдет в приложении А. Восьми вершинам куба присвоены разные цвета спектра - черный, белый, красный, зеленый, синий, бирюзовый, фиолетовый и желтый. В программе установлен режим гладкого закрашивания, и OpenGL автоматически выполняет интерполяцию цвета по мере перехода от одной вершины к другой.
Рис. 6.30. Определение нормали, ассоциируемой с вершиной полигональной сети
6.5.3. Закрашивание по методу Фонга Но даже при использовании метода Гуро в ряде случаев не удается избежать появления на изображении полос Маха. Фонг предложил интерполировать не цвет точек от вершины к вершине, а направление нормалей последовательных точек на ребрах каждого многогранника. Рассмотрим отдельный многоугольник полигональной сети, представленный на рис. 6.33. С каждой вершиной можно связать нормаль, которая формируется усреднением нормалей к граням, пересекающимся в этой вершине. Далее с помощью билинейной интерполяции, которую мы уже рассматривали в главе 4, можно интерполировать нормали по всей внутренней области многоугольника. Рассмотрим рис. 6.33. Векторы нормалей в вершинах А и В используются для интерполяции вдоль ребра, связывающего эти две вершины:
