6.5. Закрашивание многоугольников 267
Рис. 6.26. Удаленные источник света и наблюдатель
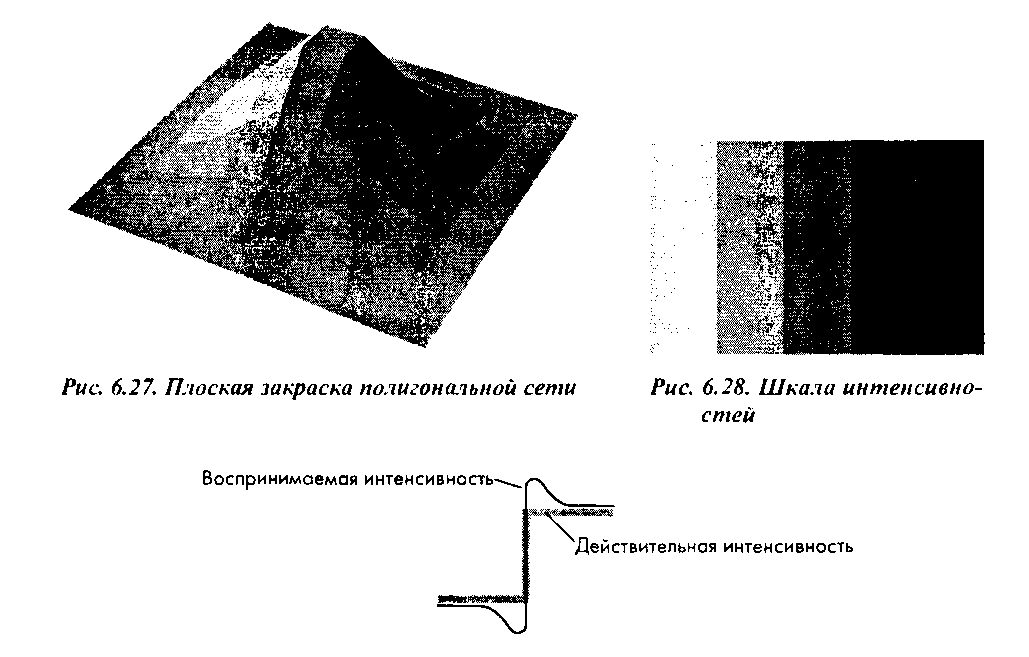
Рис. 6.29. Воспринимаемая и действительная интенсивности в области перепада
6.5.2. Интерполяционное закрашивание и закрашивание по методу Гуро В программе отображения вращающегося куба (см. главу 4) мы уже использовали средства интерполяции цвета, ассоциированного с отдельными вершинами многоугольника, которыми располагает система OpenGL. Если установить режим сглаживания при закрашивании, передав в качестве аргумента функции glShadeModel( ) значение GL_SM00TH, то OpenGL будет интерполировать цвет вдоль отображаемого примитива, например прямой. Предположим, что в программе установлены режимы сглаживания закрашивания и учета освещения и что с каждой вершиной ассоциирован вектор нормали соответствующего многоугольника. При вычислении освещения каждой вершины определяется ее цвет, который зависит от свойств материала и векторов v и 1, вычисленных раньше для этой вершины. Обратите внимание на то, что при использовании удаленных источников света и отсутствии зеркальной составляющей алгоритм интерполяционного закрашивания сформирует одинаковый цвет для всей внутренней области многоугольника.
Возвращаясь к полигональной сети, отметим, что идея использования в вычислениях нормалей, ассоциированных с вершинами такой сети, должна вызвать у любого математика возражения, поскольку с математической точки зрения она абсолютно некорректна. Поскольку вершина является точкой пересечения, как минимум, двух по-разному ориентированных многоугольников, то в ней происходит разрыв непрерывности функции вектора нормали. Хотя такая ситуация и может серьезно осложнить математику алгоритма. Гуро (Gouraud) пришел к выводу, что нормаль в точке вершины может быть определена таким способом, который позволит сгладить закрашивание. Рассмотрим одну из вершин в середине сети, в которой пересекаются четыре многоугольника (рис. 6.30). Каждый многоугольник имеет свой вектор нормали. Метод закрашивания Гуро состоит в том, что с вершинами связываются нормали, которые получаются в результате усреднения нормалей многоугольников, пересе-
