п(а) = (\-а)пА + апИ.
6.5. Закрашивание многоугольников
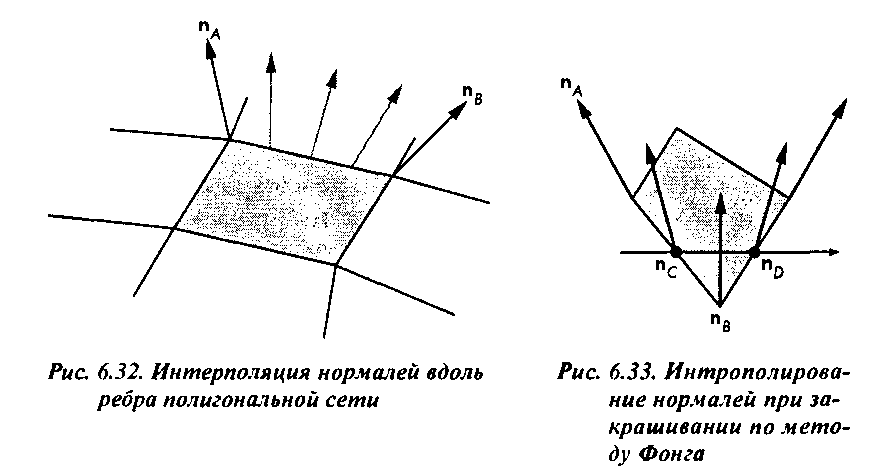
Аналогичную процедуру можно выполнить и для других ребер многоугольника. Затем можно вычислить нормаль в любой точке внутренней области этого многоугольника, зная распределение нормалей на его ребрах: п(а, Р) = (1-Р)пг + рП/> Получив вектор нормали в определенной точке, можно выполнить все необходимые вычисления, определяемые используемой моделью отражения. Обычно этот процесс реализуется вместе с растровым преобразованием многоугольника, в результате чего отрезок между точками С и D проецируется на участок строки развертки в буфере кадра. Мы рассмотрим эту тему подробнее в главе 7.
Метод Фонга позволяет получить более гладкое тонирование изображения, но за это приходится платить весьма изрядную цену - объем вычислений резко возрастает (см. упр. 6.23). Существует множество вариантов аппаратной реализации метода Гуро, которые позволяют получать изображение приемлемого качества, практически не увеличивая время закрашивания, чего не скажешь о методе Фонга. В результате в настоящее время метод Фонга используется только в тех системах, где не требуется формировать изображение в реальном масштабе времени.
6.6. Аппроксимация сферической поверхности рекурсивным разбиением Для демонстрации того, как на практике реализуются различные методы закрашивания криволинейных поверхностей в графической системе, следовало бы использовать сферу. Однако объект этого типа в OpenGL непосредственно не поддерживается. В библиотеках утилит GL (GLU) и инструментальных средств GL (GLUT) имеются различные варианты аппроксимации сферы. В первой используется квадратичная аппроксимация (эту тему мы обсудим в главе 10), а во второй - полигональная.
В этом разделе будет рассмотрен упрощенный алгоритм полигональной аппроксимации, на основе которого мы разработаем программу и продемонстрируем, как параметры закрашивания связываются в программе с полигональной аппроксимацией криволинейных поверхностей. Вы познакомитесь с методикой рекурсивного разбиения, которая позволяет аппроксимировать кривые и криволинейные поверхности с любой заданной точностью.
