X = ап + р..
Учитывая, что вектор I должен иметь единичную длину, получим
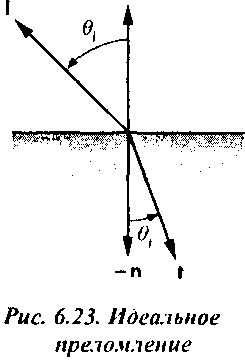
светового луча
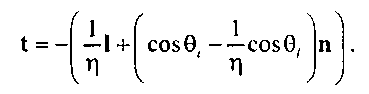
Знак "минус" в этом уравнении появился вследствие того, что вектор t направлен в сторону внутреннего полупространства поверхности раздела сред. Угол, при котором подкоренное выражение для cos0, становится равным нулю, т.е. выполняется условие sin0/ = Tj, называется критическим углом (critical angle). Если на поверхность раздела сред свет падает под этим углом, возникает явление полного внутреннего отражения, т.е. преломленный луч направляется вдоль поверхности раздела. При дальнейшем увеличении 0/ весь падающий световой поток будет отражаться от поверхности раздела сред.
Более общий случай того, что происходит на границе раздела двух сред, представлен на рис. 6.24: часть падающего светового потока преломляется, часть отражается как при зеркальном отражении, а остальная часть поглощается. Распределение по направлениям той части светового потока, которая прошла во вторую среду, имеет такой же характер, как и в слу6.4. Вычисление векторов чае зеркального отражения, но лучи концентрируются в окрестности вектора t. Следовательно, модель преломления для наблюдателя, расположенного со стороны внутреннего полупространства поверхности раздела, может включать член, пропорциональный скалярному произведению t v. При моделировании преломления можно воспользоваться описанной выше методикой использования вектора половинного направления, что позволит несколько упростить вычисления (см. упр. 6.16).
Рис. 6.24. Реальная картина взаимодействия света с границей раздела двух сред
6.5. Закрашивание многоугольников Располагая средствами вычисления векторов нормали, можно при заданном расположении источников света и наблюдателя применить рассмотренные модели ко всем точкам поверхностей объектов сцены. Но, к сожалению, использование уравнений вычисления нормали, которые мы рассмотрели в разделе 6.4 применительно к сферической поверхности, приводит к неприемлемо большим вычислительным затратам. Раньше мы неоднократно подчеркивали достоинства полигональной модели для представления объектов отображаемой сцены. Использование этой модели для выполнения тонирования изображения сцены, состоящей из множества криволинейных объектов, существенно уменьшает объем вычислений. Именно такая модель, предполагающая аппроксимацию криволинейных поверхностей множеством маленьких плоских многоугольников, и используется в большинстве графических систем, в том числе и в OpenGL.
