Если удастся заменить вычисление скалярного произведения г v произведением п h, можно избавиться от вычисления вектора г. Однако угол \\f меньше угла ф, а следовательно, Рис. 6.22. Определение вектора половинного направления
Закрашивание
если использовать тот же показатель степени е в выражении (п h)4, который использовался в члене (г v)c', то интенсивность зеркальной составляющей уменьшится. Справиться с этой проблемой можно, используя вместо исходного значения е скорректированное значение е', такое, что (п h)4' будет достаточно близким к (г \)1'. Думаю, не стоит доказывать вам, насколько желательно уменьшить объем вычислений, но при этом нужно принимать во внимание все последствия такого упрощения для отображения при разном относительном положении источников света как плоских, так и криволинейных поверхностей (см. упр. 6.8).
6.4.4. Преломление света Аналогичная методика используется и при тонировании сцен, в которых нужно учитывать не только отражение света от границы двух сред, но и явление пропускания света из одной среды в другую (такая задача решается в простой программе трассировки лучей, которую мы рассмотрим в разделе 6.10). Рассмотрим поверхность, через которую пропускается весь падающий на нее световой поток (рис. 6.23). Если скорость распространения света в двух средах отличается, то на границе этих сред происходит преломление падающего светового луча. Пусть т|/ и Т|, - показатели преломления (indices of refraction) - параметры, характеризующие относительную скорость распространения света в средах по обе стороны от поверхности их раздела. Закон Снелля (Snell'z law) (см. упр. 6.13) утверждает, что
sin 0, _ г|, sin 0, г), Направление преломленного луча t находится следующим образом. Значение cosG/ определяется векторами п и 1; если они нормализованы, то cosG/ равно скалярному произведению этих векторов. По заданному значению cos9, можно найти sin0„ а далее, зная характеристики обеих сред, - и sin9/. Обозначив г) = Г),/г)/, получим
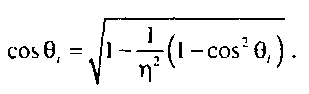
Как и при вычислении компонентов отраженного луча, в случае преломления векторы I, п и 1 должны быть компланарны, следовательно,
