6.4. Вычисление векторов
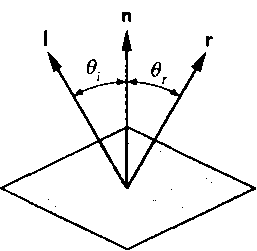
Рис. 6.21. Отражение от идеального зеркала В двухмерном пространстве направление отраженного луча задается этим законом однозначно, а в трехмерном пространстве для вычисления направления соответствующего вектора нужно ввести дополнительное условие - в точке р поверхности падающий и отраженный лучи, а также нормаль к поверхности должны лежать в одной плоскости, т.е. быть компланарными векторами. В совокупности эти два условия позволяют однозначно определить направление отраженного луча г по заданным вектору нормали п и орту падающего луча 1. Поскольку нас интересует только направление отраженного луча г, то в дальнейшем будем предполагать, что все интересующие нас векторы являются ортами - векторами единичной длины, т.е. |1| = |п| = 1. На искомый вектор также накладывается условие |r| = 1 .Если 6, = 9„ то cosö, = cos9r. Используя скалярное произведение, получим соотношение, связывающее углы падения и отражения"images/tmpB6CA-261.png">
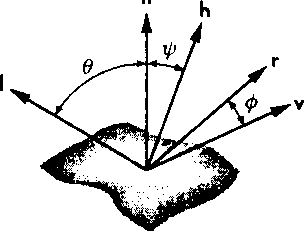
На рис. 6.22 представлены все пять векторов, которые понадобятся нам для выполнения тонирования изображения поверхности. На этом чертеже угол \|/ между векторами п и h называется углом половинного направления (half-angle). Если вектор v лежит в той же плоскости, что и 1, п и г, то выполняется соотношение (см. упр. 6.7) 2\|/ = ф.
