х' = х, у' = у, г' = аг + Р, м'' - -г.
После деления на м-' получим координаты точки в трехмерном пространстве
, x . V „ (х =-, у =--, :. =- а + - .
Если применить по отношению к N преобразование ортогонального проецирования вдоль оси г, получим в результате матрицу
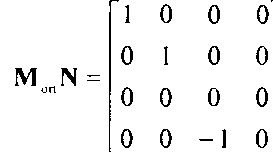
которая и является матрицей простого перспективного преобразования. Проекция произвольной точки р имеет вид После выполнения перспективного деления получим искомые значения л'/; и \у.
Итак, мы показали, что если применить к произвольной точке преобразование 14, то ее ортогональная проекция будет иметь такой же вид, как и перспективная проекция исходной точки. Здесь есть аналогия с применением преобразования скоса на первом этапе приведения косоугольной проекции к ортогональной.
Матрица N является невырожденной и преобразует исходную зону видимости в новую. Параметры а и Р можно выбрать таким образом, чтобы новая зона имела вид канонической. Рассмотрим уравнения ограничивающих плоскостей х = ±г. Эти плоскости преобразуются посредством х" =-х/:. в дг" = ±1. Аналогичным образом плоскости у = ±г преобразуются в у" - ±1. Передняя отсекающая плоскость зоны видимости г = гтіп преобразуется в плоскость
„ ( р ї
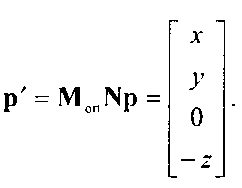
5.8. Матрицы перспективного проецирования И, наконец, задняя отсекающая плоскость зоны видимости г преобразуется в плоскость
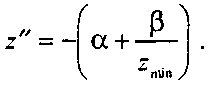
Если выбрать значения этих параметров в соответствии с соотношениями
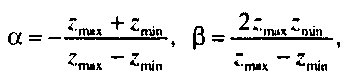
то отображением плоскости г = :min будет плоскость г" = -1, плоскости z - rmax - плоскость z" ~ 1, т.е. мы получим искомую каноническую зону видимости. На рис. 5.39 показано, как выглядит это преобразование и искажение куба внутри зоны видимости. Таким образом, N трансформирует усеченную пирамиду видимости в правильный параллелепипед, а ортогональное преобразование трансформирует параллелепипед в канонический куб видимости. В результате ортогональная проекция искаженного объекта будет иметь тот же вид, что и перспективная проекция исходного. Матрицу N называют матрицей перспективной нормализации {perspective-normalization matrix). Отображение
