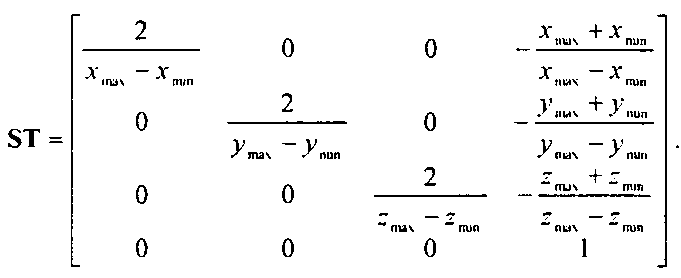
5.7. Матрицы параллельного проецирования Матрицу этого преобразования нужно вставить между матрицами скоса и конечного ортогонального преобразования: Р = MorISTH.
Значения дгтач, *min> .Утах» Jmin- это параметры правильного параллелепипеда видимости, который получится после преобразования скоса. Эти значения должна вычислить прикладная программа, взяв за основу исходную зону видимости - косоугольную призму.
5.8. Матрицы перспективного проецирования Принцип, положенный в основу реализации перспективного проецирования в OpenGL, тот же, что и в организации параллельного, - формируется преобразование, которое приводит к искажению объектов, такому, что после их проецирования стандартным способом создается нужное изображение. Для вывода вида такого преобразования сначала нужно решить, какую форму в случае перспективного проецирования должна иметь каноническая зона видимости. Затем следует сформировать преобразование перспективной нормализации {perspective-normalization transformation), которое преобразует перспективную проекцию в ортогональную. Последний этап - вывод матрицы перспективного проецирования, которая и используется в OpenGL.
5.8.1. Перспективная нормализация В разделе 5.3 была выведена матрица простого перспективного преобразования. Если уравнение картинной плоскости z = -1, а центр проецирования размещен в начале координат, то эта матрица имеет вид
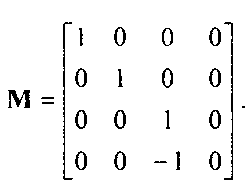
Но для формирования изображения нам нужно знать параметры зоны видимости. Предположим, что выбран угол зрения 90° и, таким образом, боковые грани зоны видимости наклонены по отношению к картинной плоскости на 45°. Следовательно, зона видимости имеет вид пирамиды бесконечной в одном направлении, грани которой - плоскости х = ±:, у = ±г (рис. 5.38).
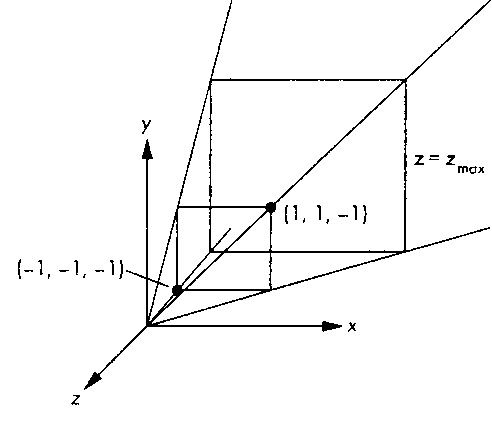
Рис. 5.38. Простая перспективная проекция Эту зону можно ограничить, задав переднюю и заднюю отсекающие плоскости г = г„ гтач, где оба значения отрицательны, причем гтач > гт|П.
Визуализация
Рассмотрим матрицу
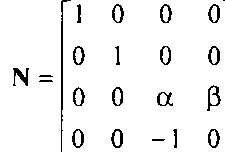
которая аналогична М, но не является вырожденной. Пока что не будем рассматривать, каковы должны быть значения а и (3, - главное, что они должны быть отличны от 0. Если применить преобразование N к точке в однородных координатах р = [х у 2 1]', то получим новую точку ц г- [л-' у' г' іг]7, где
