является нелинейным, но сохраняет порядок расположения точек по глубине. Так, если г, и z1 - значения глубины расположения двух точек до преобразования и г, > г2, то после преобразования выполняется соотношение г" >г"2.
Следовательно, алгоритм удаления невидимых поверхностей, основанный на анализе глубины, будет успешно работать и после выполнения перспективной нормализации, хотя нелинейность и может привести к некоторым проблемам с точностью вычислений, так как буфер глубины имеет ограниченную разрядность (обычно - 24 или 32 бита).
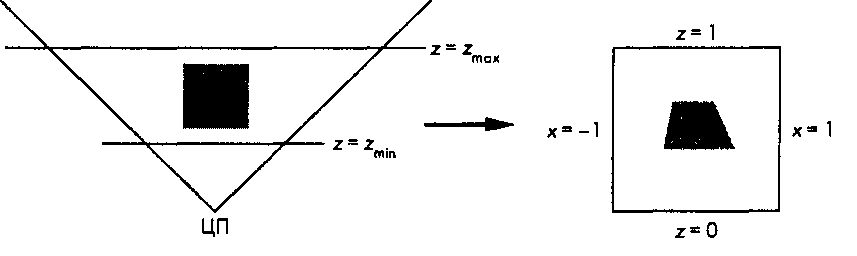
Рис. 5.39. Перспективная нормализация зоны видимости Итак, мы показали, как с помощью предварительного искажения можно свести и перспективное, и параллельное проективные преобразования к ортогональному. Такая замена позволяет включить любой тип проективного преобразования в стандартный процесс конвейерной обработки. Все детали реализации конвейера мы рассмотрим в главе 7, где будет показано, что возможность привести зону видимости любого типа к параллелепипеду также упрощает и выполнение отсечения, и удаление невидимых поверхностей.
5.8.2. Перспективное преобразование в OpenGL
При использовании функции glFrustum( ) зона видимости не обязательно должна иметь форму симметричной (правильной) усеченной пирамиды. Геометрический смысл аргументов вызова этой функции поясняет рис. 5.40. Матрица перспективного преобразования OpenGL формируется таким образом, что сначала заданная усеченная пирамида трансформируется в симметричную с углом на-
Визуализация

клона боковых граней 45° (см. рис. 5.38). Этот процесс аналогичен трансформации косоугольной призмы видимости в ортогональный параллелепипед. Первый этап трансформации - преобразование скоса, превращающее асимметричную пирамиду в симметричную. Угол скоса должен быть таким, чтобы точка ((х^п + *тахУ2, (у,™ + УтпУ2. г,™) заняла положение (0, 0,2^п). Таким образом, матрица скоса определяется в соответствии с соотношением

Полученная в результате усеченная пирамида видимости имеет следующие плоскости граней"opengl5_256.html">⇐ Предыдущая| |Следующая ⇒
