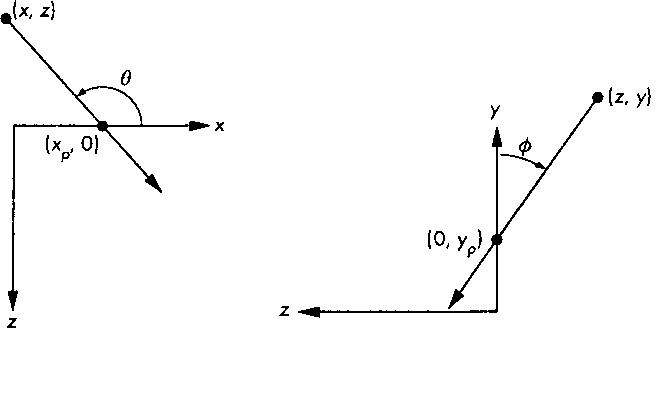
5.7. Матрицы параллельного проецирования ной проекции имеет переднюю и заднюю грани, параллельные картинной плоскости, а боковые- верхнюю и нижнюю, параллельные проецирующим лучам (рис. 5.35). Анализируя вид сверху и сбоку на рис. 5.36, выведем уравнения косоугольной проекции.

Проекция характеризуется углами 0 и ф. В техническом черчении широко используются частные виды косоугольных проекций - кавальерная и кабинетная, - которые характеризуются конкретными значениями этих углов. Однако эти углы не являются единственно возможным набором параметров, характеризующих косоугольную проекцию (см. упр. 5.9 и 5.10).

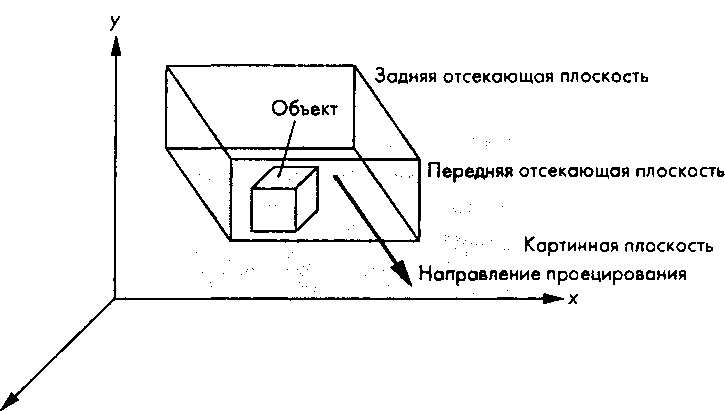
Рис. 5.35. Зона видимости при косоугольном проецировании

а) б)

Рис. 5.36. Косоугольное проецирование"images/tmpB6CA-213.png">

где Н(9, ф) является матрицей преобразования скоса. Таким образом, косоугольное проецирование можно представить как первоначальный скос объектов посредством Н(9, ф), а затем выполнение обычного ортогонального проецирования. На рис. 5.37 показано, как матрица Н(в, ф) преобразует объект (куб) внутри зоны видимости. Боковые грани зоны видимости становятся перпендикулярными картинной плоскости, а боковые грани куба-наклонными по отношению к ней, поскольку на оба объекта воздействует то же самое преобразование скоса. Следовательно, ортогональная проекция искаженного куба будет выглядеть точно также, как и косоугольная проекция неискаженного.

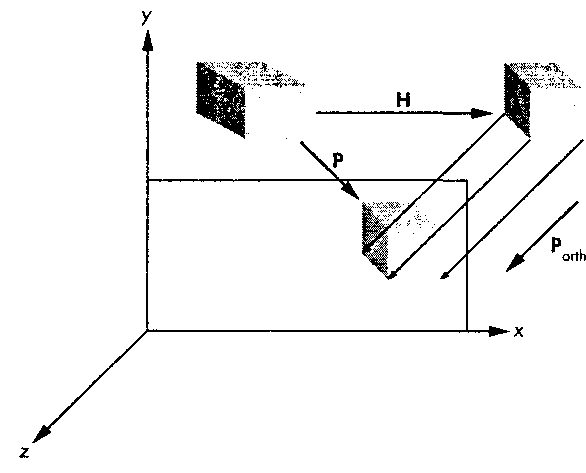
Рис. 5.37. Эффект от преобразования скоса Но мы еще не закончили, поскольку созданная после скоса зона видимости еще не является канонической. Теперь воспользуемся преобразованиями масштабирования и сдвига, выведенными в предыдущем разделе"opengl5_253.html">⇐ Предыдущая| |Следующая ⇒