Объекты и геометрические преобразования
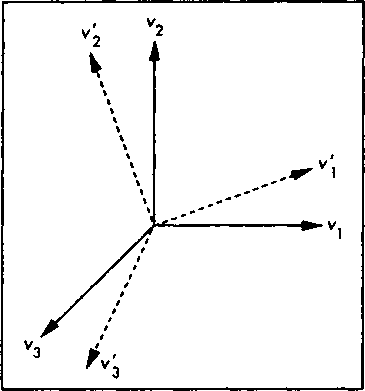
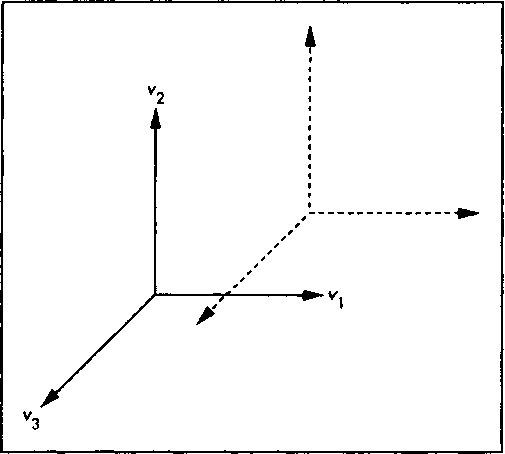
Рис. 4.19. Поворот и масштабирование базиса Рис 4.20. Плоскопараллельное смещение базиса
4.3.2. Пример изменения представления Предположим, что имеется вектор и», представление которого в некотором базисе имеет вид
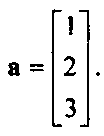
Обозначим три вектора базиса3 соответственно v,, у2, у3. Тогда Ь' = у| + 2г2 + Зу3.
Теперь предположим, что возникла необходимость сформировать новый базис на основе прежнего"images/tmpB6CA-114.png">
Матрица преобразования представления из базиса {у,, у2, V]} в базис {м,, и2, м3} имеет вид
3 Если мы работаем в метрическом трехмерном пространстве (Я3), а не в абстрактном, то можно ассоциировать базис V/. \2, Уз с единичным базисом в
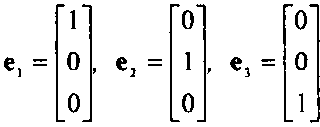
4.3. Системы координат и фреймы
A=(Mr)"' =| "l |
Г |
-і | і | -1 1' | |
| і | = | 1 -1 | |||
| і | 0 1 |
В новой системе координат представление будет иметь вид "-Г
Ь = Аа =
Отсюда следует, что
w =-м| -и2 + Зм3.
4.3.3. Однородные координаты
Когда речь заходит о представлении точки Р, имеющей положение (х, у, г), с помощью трехмерного фрейма с началом в точке Р0 и базисом {уи у2, у3}, то первой приходит в голову мысль использовать матрицу-столбец
У
где х, у, 2 - компоненты базисных векторов в этой точке, т.е. коэффициенты в соотношении Р - Р0 + ХУ\ + уУ2 + 2у3.
Но в этом случае точка будет представлена так же, как и вектор
и» = 5|у| + 5гУ2 + б3у3, поскольку м> представляется столбцом '8,
W =В литературе очень часто точка (х,у, z) ассоциируется с вектором, проведенным в эту точку из начала координат. Эта ассоциация может привести к недоразумениям. Например, вектор из точки (1, 1, 1) в точку (2, 3,4) равен вектору, проведенному из точки (0, 0, 0) в точку (1, 2, 3), поскольку оба вектора имеют одинаковый модуль и направление. Но первый вектор нельзя ассоциировать с точкой (1, 2, 3) до тех пор, пока его точка приложения не будет совмещена с началом координат - точкой (0, 0,0).
Пренебрежение различием в представлении точек и векторов может серьезно усложнить реализацию системы, поскольку после этого не удастся представить смещение фрейма как все другие виды трансформаций - с помощью операции перемножения матриц. Поэтому предпочтительнее выбрать такой способ представления, который позволит легко отличать точки от векторов.
