Исключением из этого подхода является новое направление в компьютерной графике, которое получило название конструктивная геометрия тел - KIT (CSG - constructive solid geometry). В таких системах объект строится из небольшого множества монолитных (объемных) примитивов с помощью операций теории множеств, таких как объединение и пересечение. Мы вернемся к моделированию на базе конструктивной геометрии тел в главе 8. Хотя для решения задач моделирования использование концепции КГТ очень эффективно, отображать созданные модели значительно труднее, чем модели, построенные на базе полигонального разбиения поверхностей. Вполне возможно, что в будущем ситуация изменится, но сейчас мы будем уделять основное внимание методам отображения полигональных моделей объектов.
Все примитивы, с которыми приходится работать в таких моделях, описываются множествами вершин. Если перейти от абстрактных объектов к реальным, нужно сначала определиться с методами представления в графической системе вершин - точек в пространстве.
4.3. Системы координат и фреймы
В предыдущих разделах мы рассматривали точки и векторы как абстрактные объекты, не привязываясь ни к какой системе отсчета. В трехмерном векторном пространстве можно однозначно представить любой вектор м' в виде линейной комбинации любых трех линейно-независимых векторов г,, v2 и v3 (см. приложение Б):
ir = a,V| + a:v2 + a3v3.Скаляры a,, a2 и a3- это компоненты (или координаты) вектора w в базисе vu v2, v3. Это отношение показано на рис. 4.17. Можно записать представление вектора w в некотором базисе в виде матрицы, состоящей из одного столбца:
4.3. Системы координат и фреймы
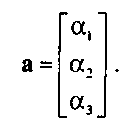
Здесь и далее буквы, набранные полужирным шрифтом, обозначают представление в определенном базисе, в отличие от абстрактного вектора который обозначается обычным шрифтом. Это же соотношение можно записать и в виде
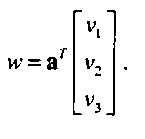
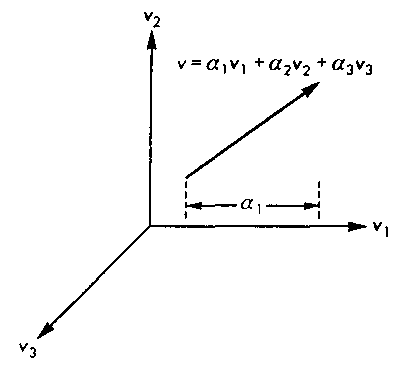
Векторы V,, г2, образующие базис, определяют конкретную систему координат. Но при рассмотрении проблем, в которых принимают участие точки, векторы и скаляры, нам потребуется более общий метод определения системы координат. Суть проблемы
