4.1.9. Плоскости Плоскость (plane) в аффинном пространстве определяется прямым расширением параметрического представления прямой. Из курса элементарной геометрии вам должно быть известно, что три точки, не лежащие на одной прямой, однозначно определяют плоскость. Предположим, что P,Q и R - это именно такие три точки в аффинном пространстве. Отрезок, который соединяет Р н Q, есть множество точек, описываемое соотношением
S(a) = аР +(\-a)Q, 0 < а < 1.
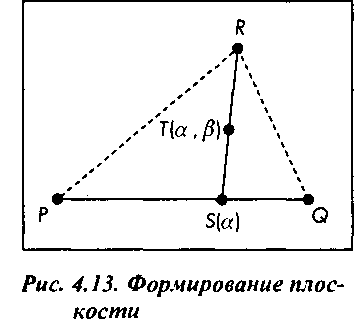
Предположим, что на этом отрезке выбрана произвольная точка и из нее проведен отрезок до точки R, как показано на рис. 4.13. Точки, расположенные на этом отрезке, можно описать, воспользовавшись вторым параметром, Р: ДР) = Р5 + (1-Р)Л, 0<р<1.
Эти точки определяются уже парой параметров - а и Р, а их совокупность образует плоскость, заданную точками Р, Q и R. Объединив два предыдущих уравнения, получим уравнение плоскости в параметрическом виде: Да, Р) = Р[а/> + (1-а)б] + (1-Р)/?.
Полученное уравнение можно переписать в другом виде: Да, Р) = /> + Р(1-а)(е-/>) + (1-Р)(Л-/>).
Учитывая, что Q-P и R-P представляют собой векторы, можно показать, что плоскость также определяется точкой Р0 и парой непараллельных векторов и и v следующим образом: Да, р) = Р0 + аи + Pv.
Несложно прийти к заключению, что при 0 < а, Р < 1 все точки Да, Р) лежат внутри треугольника, образованного вершинами P,Q и R. Если точка Р принадлежит плоскости, то Р-Р0 = аи + Pv.
Можно определить вектор п, который будет ортогонален и и, и v. Воспользовавшись векторным произведением л = м x v, получим уравнение плоскости в таком виде: п (Р-Ро) = 0.
Вектор п перпендикулярен (ортогонален) плоскости; его принято называть нормалью к плоскости. Уравнения прямых, в левой части которых стоит член Да), и плоскостей, в левой части которых стоит член Да, Р), принято называть уравнениями в параметрической форме, поскольку они определяют точки на прямой или плоскости как функции параметров аир.
4.1. Скаляры, точки и векторы
4.2. Трехмерные примитивы
В трехмерном пространстве значительно возрастает разнообразие геометрических объектов, доступных компьютерной графике. При работе на двухмерной плоскости в примерах, рассмотренных в главе 2, мы имели дело только с отрезками, плоскими кривыми и объектами, которые имели внутреннюю область, в частности многоугольниками. В трехмерном пространстве все эти типы объектов сохраняются, но, во-первых, они могут лежать в разных плоскостях, а во-вторых, к ним добавляются пространственные кривые (рис. 4.14). Помимо плоских объектов с внутренней областью, существуют и аналогичные пространственные объекты - участки криволинейных поверхностей (рис. 4.15). В трехмерном пространстве появляется совершенно новый класс объектов - объемные тела, такие как параллелепипеды и эллипсоиды (рис. 4.16).
