любую пару точек из набора {Р\, Р2,Р,,}. В геометрической трактовке выпуклая оболочка- это множество точек, принадлежащих поверхности минимальной площади, "натянутой" на заданное множество исходных точек. Понятие выпуклости играет особенно важную роль при конструировании кривых и поверхностей, и мы еще не раз вернемся к нему, в частности в главе 10.
Рис. 4.10. Выпуклая оболочка
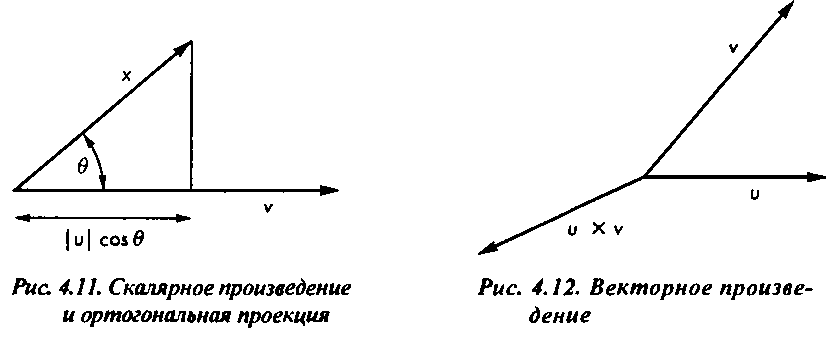
4.1.8. Скалярное и векторное произведение Многие геометрические процедуры, связанные с определением углов между векторами, реализуются с помощью элементарных операций скалярного (dot, inner) и векторного (cross) произведений двух векторов. Скалярное произведение векторов и и v обозначается и v. Если и v = 0, то и и v являются ортогональными. В Евклидовом пространстве квадрат модуля вектора есть скалярное произведение вектора на самого себя:
\и\2= и и.
Угол между двумя векторами определяется по формуле
„ «VCOS 0 = Т-Г7-Т .
мм Кроме того, выражение
I I a uv V COS 0 = -7-7-м описывает ортогональную проекцию вектора v на и, как показано на рис. 4.11.
Если в трехмерном пространстве заданы три линейно-независимых вектора, то можно с помощью операции скалярного произведения построить три вектора, каждый из которых будет ортогонален двум другим. Этот процесс рассмотрен в приложении Б. Можно также использовать два непараллельных вектора, и и v, для того чтобы определить третий вектор п, ортогональный по отношению к первым двум (рис. 4.12). Этот вектор задается с помощью операции векторного произведения (cross product), формальное определение которой приведено в Приложении В: п = и х V.
154 Глава 4. Объекты и геометрические преобразования
Модуль векторного произведения позволяет определить синус угла 9 между векторами-сомножителями и И v.
i i |"ху|
мм Обратите внимание на то, что векторы и, v и п образуют правостороннюю систему координат (right-handed coordinate system), т.е. если вектор и направлен в ту же сторону, что и большой палец правой руки, а вектор v будет направлен вдоль указательного пальца, то вектор п будет параллелен среднему пальцу.
