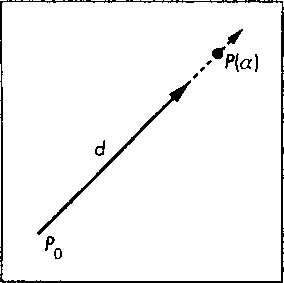
Рис. 4.7. Определение прямой в аффинном пространстве
Объекты и геометрические преобразования
4.1.6. Аффинное сложение В аффинном пространстве определены операции сложения двух векторов, умножения вектора на скаляр и сложения вектора и точки, а операции сложения произвольных точек и умножения точки на скаляр отсутствуют. Но в этом пространстве существует также операция аффинного сложения {affine addition), в которой имеются некоторые элементы двух последних операций. Для любой точки Q, вектора v и положительного скаляра а результат операции Р = Q+av
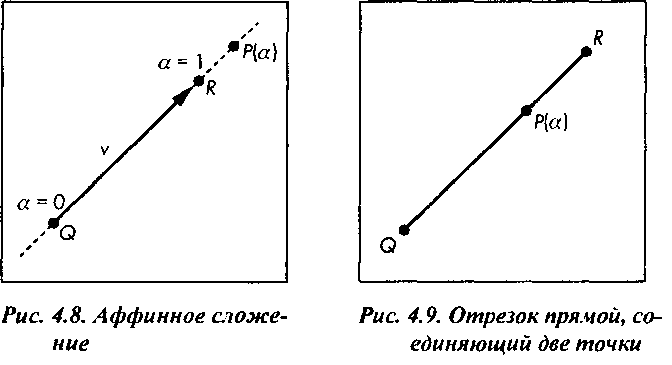
описывает все точки на прямой, проходящей через точку Q в направлении вектора v (рис. 4.8). Всегда можно найти такую точку R, что
v = R-Q.Следовательно,
P = Q + a(R-Q) = aR + (\-a)Q.Эта операция выглядит так же, как и сложение двух точек, и, следовательно, имеет эквивалентную форму:
P = a}R + a2Q,где а, + а2 = 1.
4.1.7. Выпуклость
Выпуклым (convex) является такой объект, для которого соблюдается следующее правило: все точки, лежащие на отрезке, соединяющем две любые точки, принадлежащие объекту, также принадлежат этому объекту. Мы уже видели, на примере многоугольников (см. главу 2), насколько важна выпуклость объекта. Для более формального анализа выпуклости мы теперь можем воспользоваться операцией аффинного сложения. При 0<а<1 операция аффинного сложения определяет отрезок, связывающий точки R и Q, как показано на рис. 4.9. Следовательно, отрезок прямой является выпуклым объектом. Расширим операцию аффинного сложения и на объекты, заданные п точками Ри Р2, Р„. Рассмотрим выражение Р = а,/>, + а2Р2 + .. +а,Л-
Можно доказать по индукции, что эта сумма определена тогда и только тогда, когда а, + а2 + … + а„= 1.
4.1. Скаляры, точки и векторы
Множество точек, образованных аффинным сложением п точек, на которое распространяется дополнительное ограничение а,>0, /=1,2,и, называется выпуклой оболочкой (convex hull) исходного набора точек (рис. 4.10). Несложно доказать по индукции, что выпуклая оболочка включает все отрезки прямых, связывающих
