Пример реализации этого алгоритма можно найти в [8] и [15].
10.3.2. Количественная невидимость. Алгоритм Аппеля Рассмотрим произвольное гладкое выпуклое тело в пространстве. Взяв произвольную точку Р на границе этого тела, назовем ее лицевой, если (п, I) > 0, где п -вектор внешней нормали к границе в этой точке. Если же (п, I) < 0, то данная точка является нелицевой (и, соответственно, невидимой). В силу гладкости поверхности у лицевой (нелицевой) точки существует достаточно малая окрестность, целиком состоящая из лицевых (нелицевых) точек и проектирующаяся на картинную плоскость взаимнооднозначно (не закрывая саму себя) (рис. 10.20).
У точек, для которых (п, I) - 0, подобной окрестности (состоящей только из лицевых или только нелицевых точек) может не существовать. Такие точки, в отличие от (регулярных) точек называются нерегулярными (особыми) точками проектирования (рис. 10.21).
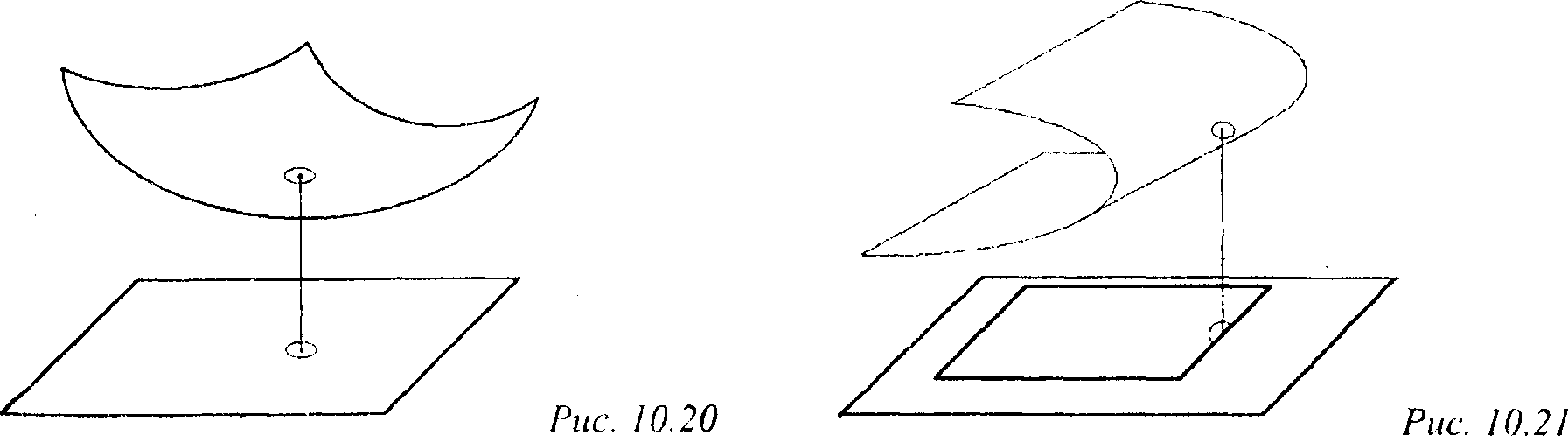
В общем случае множество всех нерегулярных точек (п,1) = 0 (13)
образует на поверхности рассматриваемого объекта гладкую кривую, называемую контурной линией. Эта линия разбивает поверхность выпуклиго тела на две части, каждая из которых однозначно проектируется гга картинную плоскость и целиком состоит из регулярных точек. Одна из этих частей является полностью видимой, а Другая - полностью невидимой.
Компьютерная графика. Полигональные модели Попытаемся обобщить этот подход на случай одного или нескольких невыпуклых тел.
Множество всех контурных линий (их уже может быть несколько) разбивает границы тел на набор связных частей (компонент), каждая из которых по-прежнему взаимнооднозначно проектируется на картинную плоскость и состоит либо из лицевых, либо из нелицевых точек.
Никакая из этих частей не может закрывать себя при проектировании, однако возможны случаи, когда одна такая часть закрывает другую. Чтобы это учесть, введем числовую характеристику невидимости - так называемую количественную невидимость точки, определив ее как количество точек, закрывающих при проектировании данную точку. Точка оказывается видимой только в том случае, когда ее количественная невидимость равна нулю.
