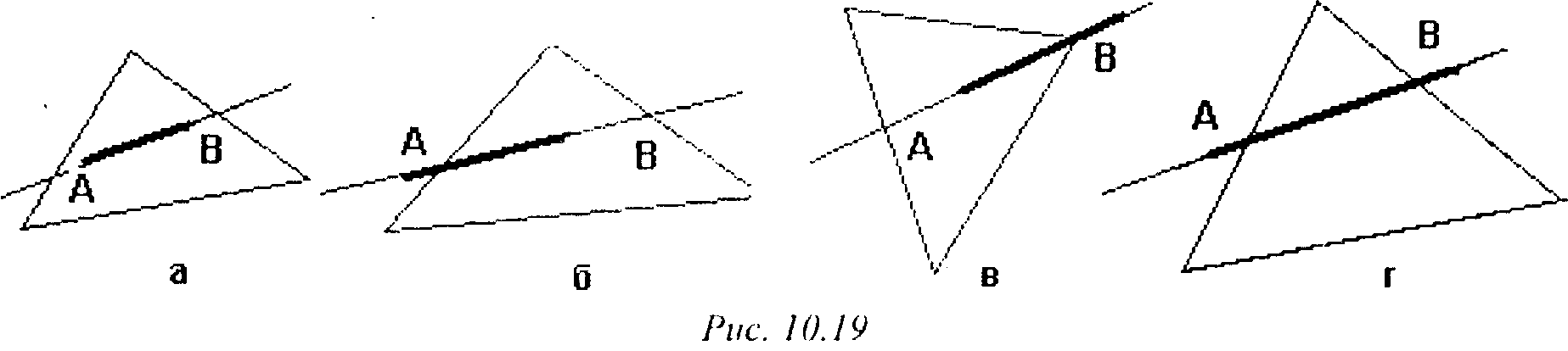
4. Прямая АВ пересекает ребра проекции грани в двух точках, причем
0 < < /2 < 1 (рис. 10.19, г). Если ребро АВ лежит дальше от картинной плоскости, чем соответствующая грань, то оно разбивается на три части, средняя из которых отбрасывается.
Для определения того, что лежит ближе к картинной плоскости - отрезок АВ (проекция которого лежит в проекции грани) или сама ірань, через эту грань проводится плоскость
(п,р) + с = 0
(/7 - нормальный вектор грани), разбивающая все пространство на два полупространства. Если оба конца отрезка А В лежат в том же полупространстве, в котором находится и наблюдатель, то отрезок лежит ближе к грани; если оба конца находятся в другом полупространстве, то отрезок лежит дальше. Случай, когда концы лежат в разных полупространствах, здесь невозможен (это означало бы, что отрезок АВ пересекает внутреннюю часть грани).
Если общее количество граней равно п, то временные затраты для данного алгоритма составляют 0(п~).
Количество проверок можно заметно сократить, если воспользоваться разбиением картинной плоскости.
10. Удаление невидимых линий и поверхностей Разобьем видимую часть картинной плоскости (экран) на х /У2 равных частей (клеток) и для каждой клетки Ац построим список всех лицевых граней, чьи проекции имеют с данной клеткой непустое пересечение.
Для проверки произвольного ребра на пересечение с гранями отберем сначала все те клетки, которые проекция данного ребра пересекает. Ясно, что проверять на пересечение с ребром имеет смысл только те грани, которые содержатся в списках этих клеток.
В качестве шага разбиения обычно выбирается 0(1), где / - характерный размер ребра в сцене Для любого ребра количество проверяемых граней практически не зависит от общего числа граней и совокупные временные затраты алгоритма на проверку пересечений составляют 0(п), где п - количество ребер в сцене.
Поскольку процесс построения списков заключается в переборе всех граней, их проектировании и определении клеток, в которые попадают проекции, то затраты на составление всех списков также составляют 0(п).
