Рассмотрим, как осуществляются эти проверки.
Пусть задано ребро АВ, где точка А имеет координаты {хш уа), а точка В - (хь, уь). Прямая, проходящая через отрезок АВ, задается уравнениями х~ха +*{ХЬ ~ха\
У = Уа +*{УЬ ~Уа\ причем сам отрезок соответствует значениям параметра 0 < t < 1. Данную прямую можно задать неявным образом как F(x, у) = 0, где
F(X, у) = {уЬ- У Ж* -Хъ)-(УЪ- *а) (У - .Уа)Предположим, что проекция грани задается набором проекций вершин Рь Л< с координатами (х,, у,), i= 1, …, и. Обозначим через F, значение функции F в точке Рх и рассмотрим z-й отрезок проекции грани Р,Р,. |. Этот отрезок пересекает прямую АВ тогда и только тогда, когда функция F принимает значения разных знаков на концах этого отрезка, а именно при Случай, когда Fr,j - 0, будем отбрасывать, чтобы дважды не засчитывать прямую, проходящую через вершину, для обоих выходящих из нее отрезков. Итак, мы считаем, что пересечение имеет место в двух случаях:
F,>ft/v,<0, Ft < 0, Fh , > 0.Точка пепесечения оппелеляется соотношениями
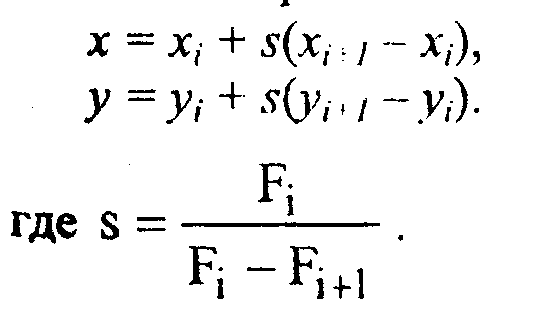
Отсюда легко находится значение параметра /:
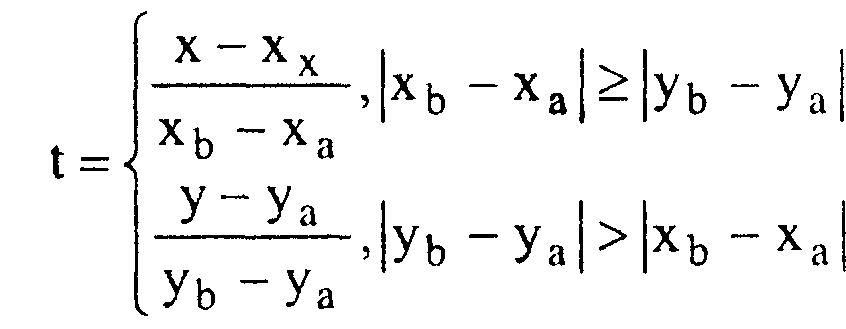
Возможны следующие случаи:
1. Отрезок не имеет пересечения с проекцией грани, кроме, быть может, одной точки. Это может иметь место, когда прямая Л# не пересекает ребра проекции (рис. 10.18, д); Компьютерная графика. Полигональные модели
прямая АВ пересекает ребра в двух точках / и /2, но либо / < 0, /2 < 0, либо / > 1, Л>> 1 (рис. 10.18,0);
прямая АВ проходит через одну вершину, не задевая внутренности треугольника (рис. 10.18, в).
Очевидно, что в этом случае соответствующая грань никак не может закрывать собой ребро АВ.
2. Проекция ребра полностью содержится внутри проекции грани (рис. 10.19, а). Тогда есть две точки пересечения прямой АВ и границы грани и / < 0 < 1 < /2. Если грань.лежит ближе к картинной плоскости, чем ребро, то ребро полностью невидимо и удаляется.
3. Прямая АВ пересекает ребра проекции грани в двух точках и либо
/] < 0 < Ґ2 ^ 1 , либо 0 < < 1 < ?2 (Рис- Ю.19, би в ). Если ребро Л/3 находится дальше от картинной плоскости, чем соответствующая грань, то оно разбивается на две части, одна из которых полностью закрывается гранью и потому отбрасывается. Проекция второй части лежит вне проекции грани и поэтому этой гранью не закрывается.
